Тема: Решение квадратных неравенств.
Цели урока:
образовательная: систематизация, обобщение знаний учащихся; проверка уровня усвоения темы;
развивающая: развитие памяти, внимания, логического мышления;
воспитательная: активизация мыслительной деятельности в процессе выполнения заданий.
Оборудование: компьютер, интерактивная доска, лист с самостоятельной работой.
Тип урока: урок обобщения и систематизации знаний.
Ход урока.
Организационный момент.
Устная работа.


Игра «Ромашка». (Слайд № 3) На доске прикреплена ромашка, на лепестках которой с обратной стороны написаны разные неравенства. Нужно определить, какие неравенства являются квадратными:
Ответ: 1, 4, 7,8.
(Слайд № 4). На доске написано решение одного квадратного неравенства. Внимательно посмотрите на ход решения и ответьте на вопросы.

Решение.
Квадратное уравнение  имеет два различных корня
имеет два различных корня  . Следовательно, квадратный трехчлен можно разложить на множители:
. Следовательно, квадратный трехчлен можно разложить на множители:  .
.
Поэтому данное неравенство имеет вид  .
.
Рассмотрим случай, когда оба множителя положительны, то есть
 . Для этого составим и решим систему:
. Для этого составим и решим систему:

Рассмотрим второй случай, когда оба множителя отрицательны, то есть  . Для этого составим и решим систему:
. Для этого составим и решим систему:

Следовательно, решениями неравенства являются числа  .
.
Ответ: 
- Какой ход решения, обозначенный , пропущен? (Произведение двух множителей положительно, если они имеют одинаковые знаки.)
- Правильно ли решена первая система? (Нет, правильный ответ  .)
.)
- Каким способом можно найти корни квадратного уравнения, с помощью которого преобразуется неравенство? (Это можно сделать с помощью формулы дискриминанта и теоремы, обратной теореме Виета; методом выделения полного квадрата.)
- Обязательно ли для решения квадратного неравенства составлять две системы неравенств? Свой ответ поясните. (Только составление двух систем позволяет найти все значения неизвестного, которые являются ответом квадратного неравенства.)
Какие из чисел 0, – 1, 2 являются решениями неравенства? (Слайд № 5).
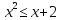 . Преобразуем неравенство:
. Преобразуем неравенство: 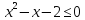 .
.
Число 0 является решением неравенства, так как при  получаем
получаем  .
.
Число – 1 является решением неравенства, так как при  получаем
получаем  .
.
Число 2 является решением неравенства, так как при  получаем
получаем  .
.
Следовательно, все из перечисленных чисел являются решениями неравенства 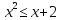 .
.
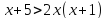 . Преобразуем данное неравенство:
. Преобразуем данное неравенство:


 / : (-1)
/ : (-1)
 .
.
Число 0 является решением неравенства, так как при  получаем
получаем  .
.
Число – 1 является решением неравенства, так как при  получаем
получаем  .
.
Число 2 не является решением неравенства, так как при  получаем
получаем  .
.
Следовательно, решениями неравенства 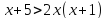 являются только числа 0 и – 1.
являются только числа 0 и – 1.
Выполнение заданий.
(Слайд № 6). На доске изображен квадрат с числами, которые являются решениями неравенства
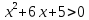 . Но среди них попало число, которое таковым не является. Найдите это число.
. Но среди них попало число, которое таковым не является. Найдите это число.
| – 6 | 4 | – 9 | 0 |
| – 10 | 2 | 6 | 3 |
| 1 | 7 | – 2 | – 8 |
| 8 | – 7 | 9 | 5 |
Решение.
Решим неравенство: 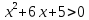

 .
.
Отсюда и
Решением первой системы является , а решением второй системы
.
И так как ,
, то в квадрате из всех написанных чисел лишнее число –2.
Ответ: – 2.
(Слайд № 7). Решите неравенство
Решение.

Отсюда
Решим первую систему неравенств:
– 2 x
Следовательно, решениями неравенства являются все числа интервала (– 2; 2).
Ответ: (– 2; 2).
(Слайд № 8). Найдите все решения неравенства , принадлежащие промежутку [1; 5].
Решение.
Следовательно, решениями неравенства, принадлежащие промежутку [1; 5], является промежуток (2; 5].
Ответ: (2; 5].
(Слайд № 9). При каких положительных значениях x верно неравенство
?
Решение.
Следовательно, неравенство верно и соответствует условию задачи при
.
Ответ:
Ответ: x 3
При каких значениях x квадратный трехчлен
принимает значения меньше 6? (Слайд № 10).
Решение.
По условию задачи составим неравенство и решим ее:
Значит, при
квадратный трехчлен
принимает значения меньше 6
Ответ:
Устная работа.
(Слайд № 11). Построить алгоритм решения квадратного неравенства методом интервалов. Учащийся на доске записывает этот алгоритм.
Ответ:
Найти корни квадратного уравнения (найти
).
Отметить найденные корни на числовой оси.
Определить знак одного из интервалов.
Расставить поочередно знаки произведения в интервалах.
(Слайд № 12). Расшифровать текст, расставив вместо звездочек нужные слова и числа.
Решение.
(
)
Так как выражение при * (всех) значениях х, то и неравенство
будет верно при * (всех) значениях х.
Ответ: х – * (любое число)
Конкурсное задание (Слайд № 13).. На доске «висят» «грибочки», которые следует собрать в несколько «корзинок». Каждая «корзинка» - определенное квадратное неравенство. «Грибочки» - числовые промежутки. Поэтому «грибочки» должны быть «помещены «только в свою корзину.
Цель: отработка умения устно решать несложные квадратные неравенства.
Подсказка: использовать числовые оси для удобства.
Корзинки:
Грибочки
Для первой корзинки:
Для второй корзинки:
Для третьей корзинки:
Физкультминутка:
Сложить руки в замок, обхватить ими затылок, направить локти вперед. Подтянуть голову к локтям, не сопротивляясь, растягивать шейный отдел позвоночника. Тянуть 10-15 секунд.
Растереть ладонями уши – сначала мочки, а затем все ухо целиком, вверх-вниз, взад-вперед.
Решение задач.
(Слайд № 14).Мальчик попал в волшебную страну, где ему дали решить необычную задачу. Помогите ему найти правильный ответ, если условия таковы: какое выражение больше «весит»:
Решение.
Чтобы ответить на вопрос задачи, необходимо решить два неравенства. При этом оба выражения должны быть больше нуля, потому что вес не может быть меньше нуля.
Составим и решим неравенство методом интервалов:
+ - +
-2 1 x
Отсюда .
+ - +
-1 2 x
Отсюда
Теперь соотнесем ответы, полученные при решении двух неравенств. Получается, что второе неравенство имеет решение при  . Значит, оно «весит» больше.
. Значит, оно «весит» больше.
Ответ: при
(Слайд № 15).2. При каких значениях х квадратный трехчлен
принимает отрицательные значения?
Решение.
Отрицательные значения квадратный трехчлен принимает, если он меньше нуля, то есть .
Решим неравенство методом интервалов.
+ - +
-5 8 x
Из рисунка видно, что при всех значениях от – 5 до 8 неравенство принимает отрицательные значения. Следовательно, квадратный трехчлен принимает отрицательные значения при
.
Ответ: .
(Слайд № 16). 3. Решите неравенство методом интервалов:
.
Решение.
Разложим числитель и знаменатель дроби на множители:
,
+ – + – +
-3 -1 1 4 x
Ответ: .
Самостоятельная работа (Слайд № 17).
Угадайте натурально число, если известно, что произведение исходного числа и чисел на 1 меньше и больше его меньше или равно нулю.
Решение.
Если обозначить исходное число за х, то число, меньшее на 1, будет х – 1, а большее него х+1. По условию задачи произведение чисел меньше или равно нулю. Составим и решим неравенство методом интервалов:
– + – +
-1 0 1 x
Из рисунка видно, что неравенство принимает отрицательные значения при
.
Следовательно, задуманное натуральное число равно 1.
Ответ: 1.
2. Решите неравенство несколькими способами, кроме решения с помощью построения графика квадратичной функции.
Решение.
Первый способ.
Следовательно, решением неравенства является отрезок
.
Ответ:
Второй способ.
+ – +
– 5 3 x
Следовательно,
Ответ:
Подведение итогов и выставление оценок.
Домашнее задание № 376(а, б, в), № 377, № 383.


 1096
1096 22
22









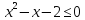 .
.  Решение квадратных неравенств
Решение квадратных неравенств 