Муниципальное бюджетное общеобразовательное учреждение
"Поповская основная общеобразовательная школа"
Гайского городского округа Оренбургской области
| «Рассмотрено» на заседании Методического совета МБОУ «Поповская ООШ» Протокол № 1 от 31.08.2017 г.
| «Согласовано» Заместитель директора по УВР
________________И.В. Знатнова
«__»____________2018г.
| «Утверждаю» Директор МБОУ «Поповская ООШ» _____________Т.С.Крылова
Приказ № 67-п от 31.08.2017 г.
|
РАБОЧАЯ ПРОГРАММА ПЕДАГОГА
Асмолова Елена Владимировна, высшая категория
Алгебра, 7 класс
2018 - 2019 учебный год
1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по алгебре для 7 класса составлена на основе Федерального государственного образовательного стандарта основного общего образования.
Программа конкретизирует содержание предметных тем, предлагает распределение предметных часов по разделам курса, последовательность изучения тем и разделов с учетом межпредметных и внутрипредметных связей, логики учебного процесса, возрастных особенностей учащихся. Составление и реализация программы обеспечивается нормативными документами:
• Федеральный закон Российской Федерации от 29 декабря 2012 г. N 273-ФЗ "Об образовании в Российской Федерации"
• Федеральный государственный образовательный стандарт основного общего образования, утвержденный приказом Министерства образования и науки РФ от 17 декабря 2010 № 1897
• Примерные программы по учебным предметам
• Примерная образовательная программа основного общего образования
• Основная образовательная программа основного общего образования МБОУ «Поповская ООШ»
• Федеральный перечень учебников, рекомендованных (допущенных) Министерством образования и науки РФ к использованию в образовательном процессе в общеобразовательных школах.
Общая характеристика учебного предмета
Содержание раздела «Алгебра» направлено на формирование у учащихся математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчёркивает значение математики как языка для построения математических моделей процессов и явлений реального мира.
В курсе алгебры 7 класса систематизируются и обобщаются сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной; учащиеся знакомятся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида, действиями над степенями с натуральными показателями, формулами сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители, со способами решения систем линейных уравнений с двумя переменными, вырабатывается умение решать системы уравнений и применять их при решении текстовых задач.
Изучение алгебры в 7 классе направлено на достижение следующих целей:
1) в направлении личностного развития:
развитие логического и критического мышления, культуры речи;
формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие интереса к математическому творчеству и математических способностей;
2) в метапредметном направлении:
развитие представлений о математике как о форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
3) в предметном направлении:
овладение алгебраическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Задачи:
сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить логическое мышление и речь;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Место учебного предмета «Алгебра» в учебном плане.
Согласно учебному плану МБОУ «Поповская ООШ» на изучение алгебры в 7 классе отводится 3 часа в неделю, всего 102 часа.
Возможна корректировка рабочей программы.
Для реализации рабочей программы используется учебно-методический комплект, включающий в себя: учебник Ю.Н. Макарычев, Н.Г. Миндюк и др. (Москва, Просвещение, 2017г.).
Изучение алгебры дает возможность обучающимся достичь следующих результатов развития:
в личностном направлении:
1) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контр-примеры;
2) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
3) представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
4) креативность мышления, инициатива, находчивость, активность при решении математических задач;
5) умение контролировать процесс и результат учебной математической деятельности;
6) способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
в метапредметном направлении:
1) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
2) умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
3) умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
4) умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
5) умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
7) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
8) умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
9) умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
в предметном направлении:
1) овладение базовым понятийным аппаратом по основным разделам содержания;
2) умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
3) овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем; умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;
4) овладение системой функциональных понятий, функциональным языком и символикой; умение использовать функционально-графические представления для описания и анализа реальных зависимостей;
5) овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях;
6) умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
2.Планируемые результаты освоения учебного предмета
Рациональные числа
Ученик научится:
понимать особенности десятичной системы счисления;
владеть понятиями, связанными с делимостью натуральных чисел;
выражать числа в эквивалентных формах, выбирая наиболее подходящую, в зависимости от конкретной ситуации;
сравнивать и упорядочивать рациональные числа;
выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;
использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчеты.
Ученик получит возможность научиться:
познакомиться с позиционными системами счисления с основаниями, отличными от 10;
углубить и развить представления о натуральных числах и свойствах делимости;
научиться использовать приёмы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
Действительные числа
Ученик научится
использовать начальные представления о множестве действительных чисел;
Ученик получит возможность:
развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в человеческой практике;
развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).
Алгебраические выражения
Ученик научится:
владеть понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;
выполнять преобразования выражений, содержащих степени с целыми показателями;
выполнять разложение многочленов на множители.
Ученик получит возможность:
научиться выполнять многошаговые преобразования целых выражений, применяя широкий набор способов и приёмов;
Уравнения
Ученик научится:
решать основные виды линейных уравнений с одной переменной, системы двух уравнений с двумя переменными;
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.
Ученик получит возможность:
овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
Описательная статистика
Ученик научится:
использовать простейшие способы представления и анализа статистических данных.
Ученик получит возможность:
приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы.
3. СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА АЛГЕБРЫ
Выражения, тождества, уравнения(22ч)
Числовые выражения и выражения с переменными. Простейшие преобразования выражений. Уравнение с одним неизвестным и его корень, линейное уравнение. Решение задач методом уравнений. Статистические характеристики.
Функции (11ч.).
Функция, область определения функции. Способы задания функций: аналитический, графический, табличный. График функции. Примеры функций, получаемых в процессе исследования различных реальных процессов и решения задач. Значение функции в точке. Функция у=кх+b, её свойства и график. Функция у=кх её свойства и график. Угловой коэффициент прямой. Расположение графика линейной функции в зависимости от её углового коэффициента и свободного члена.
Степень с натуральным показателем (11 ч.).
Степень с натуральным показателем и её свойства. Преобразование выражений, содержащих степень с натуральным показателем. Одночлен. Действия с одночленами (умножение, возведение в степень). Функции у=х2, у=х3, и их графики.
Многочлены (17 ч.).
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочлена на множители.
Формулы сокращённого умножения (19 ч.).
Формулы (a±b)2=a2±2ab+b2, (a-b)(a+b)=а2–b2, [(a±b)(a2+ab+b2)]. Применение формул сокращённого умножения к разложению на множители.
Системы линейных уравнений (16 ч.).
Уравнение с двумя переменными. Линейное уравнение с двумя переменными. Система уравнений с двумя переменными. Решение систем двух линейных уравнений с двумя переменными. Решение задач методом составления систем уравнений.
7. Повторение (6 ч.)
2 часа взяты из раздела «Повторение» на проведение Входной мониторинговой работы и Полугодовой контрольной работы.
Тематическое планирование
| Основное содержание по темам | Характеристика основных видов деятельности обучаюшегося |
| Выражения, тождества, уравнения – 22 ч. | |
| Числовые выражения и выражения с переменными. Простейшие преобразования выражений. Уравнение с одним неизвестным и его корень, линейное уравнение. Решение задач методом уравнений. Статистические характеристики. Повторение курса математики 6 класса. Контрольная работа № 1, 2. |
|
| Функции – 11 ч. | |
| Функция, область определения функции, Способы задания функции. График функции. Функция у=кх+b и её график. Функция у=кх и её график. Контрольная работа № 3. |
|
| Степень с натуральным показателем – 11 ч. | |
| Степень и её свойства. Одночлены. Контрольная работа № 4. |
возведение одночленов в степень. Строить графики функций у = х2 и у = х3. Решать графически уравнения х2 = кх + b, х3 = кх + b, где к и b — некоторые числа |
| Многочлены – 17 ч. | |
| Сумма и разность многочленов. Произведение одночлена и многочлена. Контрольная работа № 5. Произведение многочленов. Контрольная работа № 6. |
|
| Формулы сокращённого умножения – 19 ч. | |
| Квадрат суммы и квадрат разности. Разность квадратов. Сумма и разность кубов. Контрольная работа № 7. Преобразование целых выражений. Контрольная работа № 8. |
|
| Системы линейных уравнений – 16 ч. Повторение – 6 ч. | |
| Линейные уравнения с двумя переменными и их системы. Решение систем линейных уравнений. Контрольная работа № 9.
|
|
4. Формы контроля
| № п/п | Раздел программы | Кол-во часов | Контрольные работы | Самостоятельные работы. Тесты |
| 1. | Выражения, тождества, уравнения | 22 | 1 |
|
| 2 | Функции | 11 | 1 |
|
| 3 | Степень с натуральным показателем | 11 | 1 |
|
| 4 | Многочлены | 17 | 2 |
|
| 5 | Формулы сокращённого умножения | 19 | 2 |
|
| 6 | Системы линейных уравнений | 16 | 1 |
|
| 7 | Повторение | 6 | 1 |
|
|
| Итого | 102 | 9 |
|
5. КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
| № урока | Тема урока | Дата урока | Примечания | ||
| план | факт | ||||
| | Числовые выражения. Повторение по теме «Действия с десятичными дробями». | 3.09 |
|
| |
| | Выражения с переменными. Повторение по теме «Действия с обыкновенными дробями». | 4.09 |
|
| |
| | Выражения с переменными. Повторение по теме «Решение уравнений». | 6.09 |
|
| |
| | Допустимые значения переменных в выражениях |
|
|
| |
| | Сравнение значений выражений. Повторение по теме «Проценты». |
|
|
| |
| | Свойства действий над числами. |
|
|
| |
| | Тождества. Тождественные преобразования выражений. Повторение по теме «Решение текстовых задач». |
|
|
| |
| | Входная мониторинговая работа |
|
|
| |
| | Тождества. Тождественные преобразования выражений. |
|
|
| |
| | Тождества. Тождественные преобразования выражений. |
|
|
| |
| | Уравнение и его корни. |
|
|
| |
| | Линейные уравнения с одной переменной. |
|
|
| |
| | Решение линейных уравнений с одной переменной. |
|
|
| |
| | Решение линейных уравнений с одной переменной. |
|
|
| |
| | Решение задач с помощью уравнений. |
|
|
| |
| | Решение задач с помощью уравнений. |
|
|
| |
| | Решение задач с помощью уравнений. |
|
|
| |
| | Линейное уравнение с одной переменной, решение задач с помощью уравнений. |
|
|
| |
| | Линейное уравнение с одной переменной, решение задач с помощью уравнений. |
|
|
| |
| | Среднее арифметическое, размах и мода. |
|
|
| |
| | Медиана как статистическая характеристика. |
|
|
| |
| | Контрольная работа №1 по теме «Уравнения с одной переменной». |
|
|
| |
| | Что такое функция. |
|
|
| |
| | Вычисление значений функции по формуле. |
|
|
| |
| | График функции. |
|
|
| |
| | Прямая пропорциональность и ее график. |
|
|
| |
| | Прямая пропорциональность и ее график. |
|
|
| |
| | Линейная функция и ее график. |
|
|
| |
| | Линейная функция и ее график. |
|
|
| |
| | Построение графиков линейной функции и прямой пропорциональности. |
|
|
| |
| | Построение графиков линейной функции и прямой пропорциональности. |
|
|
| |
| | Повторительно-обобщающий урок по теме «Функции и их графики» |
|
|
| |
| | Контрольная работа № 2 по теме «Линейная функция». |
|
|
| |
| | Степень с натуральным показателем. |
|
|
| |
| | Умножение и деление степеней. |
|
|
| |
| | Умножение и деление степеней |
|
|
| |
| | Возведение в степень произведения и степени. |
|
|
| |
| | Возведение в степень произведения и степени. |
|
|
| |
| | Одночлен и его стандартный вид. |
|
|
| |
| | Умножение одночленов. Возведение одночлена в натуральную степень. |
|
|
| |
| | Умножение одночленов. Возведение одночлена в натуральную степень. |
|
|
| |
| | Функция у = х2 и ее график. |
|
|
| |
| | Функция у = х3 и ее график. |
|
|
| |
| | Контрольная работа № 3 по теме «Степень и ее свойства». |
|
|
| |
| | Контрольная работа за 1 полугодие |
|
|
| |
| | Многочлен и его стандартный вид. |
|
|
| |
| | Сложение и вычитание многочленов. |
|
|
| |
| | Сложение и вычитание многочленов. |
|
|
| |
| | Умножение одночлена на многочлен. |
|
|
| |
| | Умножение одночлена на многочлен. |
|
|
| |
| | Вынесение общего множителя за скобки |
|
|
| |
| | Вынесение общего множителя за скобки |
|
|
| |
| | Вынесение общего множителя за скобки |
|
|
| |
| | Контрольная работа № 4 по теме «Сложение и вычитание многочленов». |
|
|
| |
| | Умножение многочлена на многочлен |
|
|
| |
| | Умножение многочлена на многочлен. |
|
|
| |
| | Умножение многочлена на многочлен. |
|
|
| |
| | Умножение многочлена на многочлен. |
|
|
| |
| | Разложение многочлена на множители способом группировки. |
|
|
| |
| | Разложение многочлена на множители способом группировки. |
|
|
| |
| | Разложение многочлена на множители способом группировки. |
|
|
| |
| | Контрольная работа № 5 по теме «Произведение многочленов». |
|
|
| |
| | Возведение в квадрат суммы и разности двух выражений. |
|
|
| |
| | Возведение в квадрат суммы и разности двух выражений. |
|
|
| |
| | Возведение в куб суммы разности двух выражений. |
|
|
| |
| | Разложение на множители с помощью формул квадрата суммы и квадрата разности. |
|
|
| |
| | Разложение на множители с помощью формул квадрата суммы и квадрата разности. |
|
|
| |
| | Умножение разности двух выражений на их сумму. |
|
|
| |
| | Умножение разности двух выражений на их сумму. |
|
|
| |
| | Разложение разности квадратов на множители. |
|
|
| |
| | Разложение разности квадратов на множители. |
|
|
| |
| | Разложение разности квадратов на множители. |
|
|
| |
| | Контрольная работа №6 по теме «Формулы сокращенного умножения». |
|
|
| |
| | Преобразование целого выражения в многочлен. |
|
|
| |
| | Преобразование целого выражения в многочлен. |
|
|
| |
| | Пробный региональный экзамен |
|
|
| |
| | Преобразование целого выражения в многочлен. |
|
|
| |
| | Применение различных способов для разложения на множители. |
|
|
| |
| | Применение различных способов для разложения на множители. |
|
|
| |
| | Применение различных способов для разложения на множители. |
|
|
| |
| | Применение различных способов для разложения на множители. |
|
|
| |
| | Контрольная работа № 7 по теме «Преобразование целого выражения в многочлен». |
|
|
| |
| | Линейное уравнение с двумя переменными. |
|
|
| |
| | График линейного уравнения с двумя переменными. |
|
|
| |
| | Системы линейных уравнений с двумя переменными. |
|
|
| |
| | Способ подстановки. |
|
|
| |
| | Способ подстановки. |
|
|
| |
| | Способ подстановки. |
|
|
| |
| | Способ сложения. |
|
|
| |
| | Способ сложения. |
|
|
| |
| | Способ сложения. |
|
|
| |
| | Способ сложения. |
|
|
| |
| | Решение задач с помощью систем уравнений. |
|
|
| |
| | Решение задач с помощью систем уравнений. |
|
|
| |
| | Решение задач с помощью систем уравнений. |
|
|
| |
| | Решение задач с помощью систем уравнений. |
|
|
| |
| | Повторительно-обобщающий урок по теме «Системы линейных уравнений». |
|
|
| |
| | Контрольная работа № 8 по теме «Системы линейных уравнений». |
|
|
| |
| | Повторение по теме: «Уравнения с одной переменной. Решение задач с помощью уравнений». |
|
|
| |
| | Линейная функция. |
|
|
| |
| | Итоговая контрольная работа |
|
|
| |
| | Решение задач |
|
|
| |
График контрольных работ
| Контрольные работы | |
|
| |
| Входная мониторинговая работа | 18.09.18 |
| Контрольная работа №1 по теме: «Уравнения с одной переменной» |
|
| Контрольная работа №2 по теме: «Линейная функция» |
|
| Контрольная работа №3 по теме: «Степень и ее свойства» |
|
| Контрольная работа №4 по теме: «Сложение и вычитание многочленов» |
|
| Контрольная работа за 1 полугодие | 06.12 |
| Контрольная работа №5 по теме: «Произведение многочленов» |
|
| Контрольная работа №6 по теме: «Формулы сокращенного умножения» |
|
| Контрольная работа№7 по теме: «Преобразование целого выражения в многочлен» |
|
| Контрольная работа №8 по теме «Системы линейных уравнений» |
|
| Итоговая контрольная работа |
|
|
|
|
6. Перечень учебно-методического обеспечения
1. Алгебра: учебник для 7 класса общеобразовательных организаций / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под редакцией С.А. Теляковкого – М.: Просвещение, 2015.
2. Миндюк Н.Г. Рабочие программы. Алгебра. Предметная линия учебников Ю.Н. Макарычева и других. 7-9 классы.- М.: Просвещение, 2016
3. Макарычев Ю. Н., Миндюк Н. Г., Суворова С. Б. Изучение алгебры в 7—9 классах: пособие для учителей. М.: Просвещение, 2014
4. Миндюк Н. Г., Шлыкова И. С. Алгебра. Методические рекомендации. 7 класс. М.: Просвещение, 2016
5. Звавич Л.И., Кузнецова Л.В., Суворова С.Б. Алгебра: Дидактические материалы 7 класс. М.: Просвещение, 2014
6. Дудницын Ю.П., Кронгауз В.Л. Тематические тесты. 7 класс. М.: Просвещение, 2014
7. Миндюк Н. Г., Шлыкова И. С. Алгебра. Рабочая тетрадь. 7 класс. В 2-х ч. М.: Просвещение, 2015
8. Электронное приложение к учебнику Алгебра 7 класс, издательство Просвещение.
9. Макарычев Ю. Н., Миндюк Н. Г. Алгебра: Элементы статистики и теории вероятностей, 7—9. М.: Просвещение, 2015
7. Система оценки достижения планируемых результатов освоения предмета. Критерии оценивания.
Оценка качества освоения учебной программы включает текущий контроль успеваемости, промежуточную и итоговую аттестацию по итогам освоения дисциплины за 7 класс.
Контроль проводится в форме контрольных, самостоятельных, тестовых работ.
Оценка устных ответов обучающихся.
Ответ оценивается отметкой «5», если обучающийся:
полно раскрыл содержание материала в объеме, предусмотренном программой, показал результат обучения, в соответствии с основными показателями оценки;
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость использованных при ответе умений и навыков;
отвечал самостоятельно без наводящих вопросов преподавателя.
Возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые обучающийся легко исправил по замечанию преподавателя.
Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившие математического содержания ответа, исправленные по замечанию преподавателя.
допущены ошибки или более двух недочетов при освещении второстепенных вопросов или в выкладках, которые обучающийся легко исправил по замечанию преподавателя.
Ответ оценивается отметкой «3» в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала, имелись затруднения или допущены ошибки в определении понятий и, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
обучающийся не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность умений и навыков.
Ответ оценивается отметкой «2» в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учащимся большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов преподавателя.
Оценка контрольных, самостоятельных, тестовых работ.
Оценка «5» - ставится, если обучающийся демонстрирует знание теоретического и практического материала по теме работы, определяет взаимосвязи между показателями задачи, даёт правильный алгоритм решения, определяет междисциплинарные связи по условию задания, работа выполнена полностью, в логических рассуждениях и обосновании решения нет пробелов и ошибок, в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или недопонимания учебного материала).
Оценка «4» - ставится, если обучающийся демонстрирует знание теоретического и практического материала по теме работы, допуская незначительные неточности при решении задач, имея неполное понимание междисциплинарных связей при правильном выборе алгоритма решения задания, работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки), допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти работы не являлись специальным объектом проверки).
Оценка «3» - ставится, если обучающийся затрудняется с правильной оценкой предложенной задачи, дает неполный ответ, требующий наводящих вопросов преподавателя, выбор алгоритма решения задачи возможен при наводящих вопросах преподавателя. допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но обучающийся владеет обязательными умениями и знаниями по теме.
Оценка «2» - ставится, если обучающийся дает неверную оценку ситуации, неправильно выбирает алгоритм действий. Допущены существенные ошибки, показавшие, что обучающийся не владеет обязательными умениями по проверяемой теме в полной мере.
Оценка «1» - ставится, если обучающийся показал полное отсутствие обязательных знаний и умений по теме или значительная часть работы выполнена не самостоятельно, если обучающийся к выполнению работы не приступил.
ПРИЛОЖЕНИЕ
Контрольная работа №1 по теме «Уравнения с одной переменной»
В а р и а н т 1
1.Решите уравнение: а)  x = 12; б) 4x + 10,2=0; в) 6х-10,2 = 4х-2,2; г) 15- (3х-3) =5– 4х; д)2(х –0,5)+1= 9
x = 12; б) 4x + 10,2=0; в) 6х-10,2 = 4х-2,2; г) 15- (3х-3) =5– 4х; д)2(х –0,5)+1= 9
2.Катер прошел расстояние между пристанями по течению реки за 4 часа, а против течения- за 6 часов. Найдите собственную скорость катера, если течение реки 1,5 км/ч.
3. Таня в школу сначала едет на автобусе, а потом идет пешком. Вся дорога у нее занимает 26 мин. Идет она на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе?
4. Решите уравнение: 
5. В первом мешке в 2 раза больше муки, чем во втором. Когда из первого мешка взяли 30 кг муки, а во второй добавили 5 кг, то во втором стало муки в 1,5 раза больше, чем в первом. Сколько килограммов муки было в каждом мешке первоначально?
6. Решите уравнение 7х - (х + 3) = 3 (2х - 1).
В а р и а н т 2
1.Решите уравнение: а)  х = 18;б) 6x - 10,2 = 0; в) 5x - 4,5 = 3x + 2,5; г) 2x - (6x - 5) = 45; д)6(х+0,5)-3= 9
х = 18;б) 6x - 10,2 = 0; в) 5x - 4,5 = 3x + 2,5; г) 2x - (6x - 5) = 45; д)6(х+0,5)-3= 9
2.Какова скорость теплохода, если по течению реки он проплывает за 2ч то же расстояние, что за 4ч против течения? Скорость течения реки 3 км/ч.
3.Часть пути в 600 км турист пролетел на самолете, а часть проехал на автобусе. На самолете он проделал путь, в 9 раз больший, чем на автобусе. Сколько километров турист проехал на автобусе?
4. Решите уравнение: 
5. В первом ящике в 2 раза больше гвоздей, чем во втором. После того, как из первого ящика взяли 10 кг, а из второго 7 кг, в первом стало в 3 раза больше гвоздей, чем во втором. Сколько кг гвоздей было в двух ящиках первоначально?
6. Решите уравнение 6х - (2х - 5) = 2 (2х + 4).
Критерии оценивания
| Отметка | «3» | «4» | «5» |
| Кол- во заданий | 3 задания | 4-5 заданий | 6 заданий |
Контрольная работа №2 по теме: «Линейная функция»
Вариант 1
Постройте график линейной функции у = -2х + 1. С помощью графика найдите:
а) значение у, если х = 3;
б) значение х, если у = -1;
в) наименьшее и наибольшее значения функции на отрезке [-1 ; 2 ];
г) значения переменной х, при которых график функции расположен ниже оси Ох.
2. Найдите координаты точки пересечения прямых у = 3 – х и у = 2х.
3. а)Найдите координаты точки пересечения графика линейной функции у = 2х – 6 с осями координат.
б) определите принадлежит ли графику данной функции точка М (10; 14)
4. В одной и той же системе координат постройте графики функций :
а) у = -2х; б) у = -5
5. а) Задайте линейную функцию у = кх формулой, если известно, что ее график параллелен прямой у = 3х + 4.
б) определите, возрастает или убывает заданная вами линейная функция.
6 . При каком значении р решением уравнения 5х + ру – 3р = 0 является пара чисел (1; 1)
Вариант 2
Постройте график линейной функции у = 2х - 3. С помощью графика найдите:
а) значение у, если х = 3;
б) значение х, если у = -1;
в) наименьшее и наибольшее значения функции на отрезке [-2 ; 1 ];
г) значения переменной х, при которых график функции расположен выше оси Ох.
2. Найдите координаты точки пересечения прямых у = – х и у = х - 8.
3. а)Найдите координаты точки пересечения графика линейной функции у = - 2х + 6 с осями координат.
б) определите принадлежит ли графику данной функции точка М (15; -24)
4. В одной и той же системе координат постройте графики функций :
а) у = 2х; б) у = 4
5. а) Задайте линейную функцию у = кх формулой, если известно, что ее график параллелен прямой у = -4х + 7.
б) определите, возрастает или убывает заданная вами линейная функция.
6 . При каком значении р решением уравнения -рх + 2у + р = 0 является пара чисел ( -1;2)
Критерии оценивания
| Отметка | «3» | «4» | «5» |
| Кол- во заданий | 3 задания | 4-5 заданий | 6 заданий |
Контрольная работа № 3 по теме
«Степень и ее свойства»
Контрольная работа № 4 по теме
«Степень с натуральным показателем и ее свойства»
Вариант I
1. Выполнить действия:
а) c13∙c8; б) y23:y14; в) (2-2)3; г) (-2x5)4 д)  .
.
2. Найдите значение выражения 1-5х2 при х= -4.
3. Упростить выражение:
а) xy2z3(-2x2zy3); б) (-0,1n3)4; в) (-4c8d2)3;
г) (х-3)4 · х14; д) 1,5a2b-3 · 4a-3b4.
4. Построить график функции y = x3. По графику определите:
а) значения аргумента, при которых значение функции равно 1;
б) принадлежит ли графику точка N (-0,4; -0,64)?
5. Вычислить: а) б)
б) .
.
6. Решите уравнения:
 .
.
Вариант II
1. Выполнить действия:
а) а12∙а6; б) b18:b11; в) (3-1)-3; г) (4y5)4 д)  .
.
2. Найдите значение выражения -3х2+7 при х= -5.
3. Упростить выражение:
а) 4х5y7(-2xy2); б) (-3х5y2)3; в) (-5х4y)6;
г) (a-5)4 · a22; д) 0,4x6y-8 · 50x-5y9.
4.Построить график функции y = x2. По графику определите:
а) значения аргумента, при которых значение функции равно 4;
б) принадлежит ли графику точка А (-0,04; 0,16)?
5. Вычислить: а) б)
б) .
.
6. Решите уравнения:

Критерии оценивания
| Отметка | «3» | «4» | «5» | |
| Кол- во заданий | 3 задания | 4-5 заданий | 6 заданий | |
|
|
|
|
| |
|
Контрольная работа №4 Тема. Сложение и вычитание многочленов Вариант 1
а) б)
а) б)
а) б)
а) б)
и найдите его значение при |
Контрольная работа №4 Тема. Сложение и вычитание многочленов Вариант 2
а) б)
а) б)
а) б)
а) б)
и найдите его значение при
| |||
Критерии оценивания
| Отметка | «3» | «4» | «5» |
| Кол- во заданий | 3 задания | 4 задания | 5 заданий |
Контрольная работа №5 по теме: «Произведение многочленов»
Вариант 1
• 1. Выполните умножение:
а) (с + 2) (с - 3); б) (2а - 1) (За + 4); в) (5х - 2у) (4х - у);г) (а - 2) (а2 - 3а + 6).
• 2. Разложите на множители: а) а (а + 3) - 2 (а + 3); б) ах- ау + 5х - 5у.
3. Упростите выражение -0,1x (2х2 + 6) (5 - 4х2).
4. Представьте многочлен в виде произведения:
а) х2 - ху- 4х + 4у; б) ab - ас - bх + сх + с - 6.
5. Из прямоугольного листа фанеры вырезали квадратную пластинку, для чего с одной стороны листа фанеры отрезали полосу шириной 2 см, а с другой, соседней, - 3 см. Найдите сторону получившегося квадрата, если известно, что его площадь на 51 см2 меньше площади прямоугольника.
Вариант 2
• 1. Выполните умножение: а) (а - 5) (а - 3); б) (5х + 4) (2х - 1);
в) (3р + 2с) (2р + 4с); г) (6 - 2) (b2+ 2b - 3).
• 2. Разложите на множители: а) х (х - у) + а (х - у);б) 2а - 2b + са - сb.
3. Упростите выражение 0,5х (4х2 - 1) (5х2 + 2).
4. Представьте многочлен в виде произведения:
а) 2а - ас - 2с + с2; 6) bx + by - х - у - ах - ау.
5. Бассейн имеет прямоугольную форму. Одна из его сторон на 6 м больше другой. Он окружен дорожкой, ширина которой 0,5 м. Найдите стороны бассейна, если площадь окружающей его дорожки 15 м2.
Вариант 3

Вариант 4

Критерии оценивания
Задание 1,2
| Безошибочное выполнение (допущен один недочет) | Допущена 1 ошибка | Допущено 2 и более ошибок |
| 2 балла | 1 балл | 0 баллов |
Задание 3,4
| Безошибочное выполнение | Допущена (вычислительная) ошибка | Допущено 2 и более ошибок |
| 3 балла | 2 балла | 0 баллов |
Задание 5
| Безошибочное выполнение | Допущена (вычислительная) ошибка | Допущено 2 и более ошибок |
| 4 балла | 3 балла | 0 баллов |
На основе баллов, выставленных за выполнение всех заданий, подсчитывается первичный балл, который переводится в отметку по пятибалльной шкале, и определяется уровень достижения планируемых результатов:
| Первичный балл | 13-14 | 8-12 | 4-7 | 1-3 | 0 | |
| Уровень | высокий | повышенный | базовый | пониженный | низкий | |
| Отметка | 5 | 4 | 3 | 2 | 1 | |
|
Контрольная работа №6 по теме: «Формулы сокращенного умножения»
Вариант I 1.Преобразовать в многочлен: а) (а + 5)2; в) (2b – 1)(2b + 1); б) (3y – x)2; г) (4a + 3b)(4a – 3b). 2. Разложить на множители: а) b2 – 16; в) 49a2b4 – 100c4; б) a2 + 6a + 9; г) (x + 1)2 + (x – 1)2. 3. Упростить выражение: (a – 3)2 – 3a(a – 2). 4. Решите уравнение: а) (x – 3)2 – x(x + 2,7) = 9; б) 9y2 – 25 = 0. 5. Выполнить действия: а) (x2 + 1)(x – 1)(x + 1); б) (3a2 – 6b2)(3a2 + 6b2). 6*. Докажите неравенство: 9x2 + y2 6xy – 3. |
Вариант II 1.Преобразовать в многочлен: а) (x + 4)2; в) (3a – 2)(3a + 2); б) (y – 5x)2; г) (c – 2b)(c + 2b). 2. Разложить на множители: а) x2 – 81; в) 36x4y2 – 169c2; б) y2 – 4a + 4; г) (x + 1)2 – (x – 1)2. 3. Упростить выражение: (c + 6)2 – c(c + 12). 4. Решите уравнение: а) (x + 7)2 – (x – 4)(x + 4) = 65; б) 49y2 – 64 = 0. 5. Выполнить действия: а) (4a2 + b2)(2a – b)(2a + b); б) (b2c3 – 2a2)(b2c3 + 2a2). 6*.Докажите неравенство:4x2 +9y212xy – 0,1. | |||||
| Вариант III 1.Преобразовать в многочлен: а) (с – 7)2; в) (6x – 5)(6x + 5); б) (2m + n)2; г) (3d + 2y)(3d – 2y). 2. Разложить на множители: а) c2 – 25; в) 64c2d4 – 4n6; б) m2 + 8a + 16; г) (x + 2)2 + (x – 2)2. 3. Упростить выражение: (x – 5)2 – 4x(x + 3). 4. Решите уравнение: а) (x – 2)(x + 2) – x(x + 5) = – 8; б) 25y2 – 16 = 0. 5. Выполнить действия: а) (4y2 + 9)(2y – 3)(2y + 3); б) (7m2 – 3n3)(7m2 + 3n3). 6*. Докажите неравенство:x2 + 16y28xy – 1,4. | Вариант IV 1.Преобразовать в многочлен: а) (b – 4)2; в) (1 – 8k)(1 + 8k); б) (a + 5x)2; г) (4b + 5c)(4b – 5c). 2. Разложить на множители: а) y2 – 36; в) 16m6n2 – 81x2; б) n2 – 10n + 25; г) (x + 2)2 – (x – 2)2. 3. Упростить выражение: (y + 4)2 – 5y(y – 6). 4. Решите уравнение: а) x(x – 4) + (3 – x)(3 + x) = – 6; б) 81y2 – 100 = 0. 5. Выполнить действия: а) (9c2 + d2)(3c – d)(3c + d); б) (5x4 – 7y2)(5x4 + 7y2). 6*. Докажите неравенство:81x2 +4y2 36xy –8. | |||||
Критерии оценивания
| Отметка | «3» | «4» | «5» |
| Кол- во заданий | 3 задания | 4 задания | 5-6 заданий |
Контрольная работа№7 по теме: «Преобразование целого выражения в многочлен»
ВАРИАНТ 1
1. Преобразуйте в многочлен:
а) (а – 2)( а + 2) – 2а(5 – а)=
б) (у – 9)2 – 3у(у + 1) =
в) 3(х – 4) 2 – 3х2=
2. Разложите на множители:
а) 25х – х3= б) 2х2 – 20х + 50=
3. Найдите значение выражения а2 – 4bс, если а = 6, b = -11, с = -10
4. Упростите выражение:
(с2 – b)2 – (с2 - 1)(с2 + 1) + 2bс2 =
5. Докажите тождество:
(а + b)2 – (а – b)2 = 4аb
ВАРИАНТ 2
1. Преобразуйте в многочлен:
а) 4х(2х – 1) – (х – 3)(х + 3)
б) (х + 3)(х – 11) + (х + 6)2
в) 7(а + b) 2 – 14аb
2. Разложите на множители:
а) у3 - 49у б) -3а2 – 6аb - 3b2
3. Найдите значение выражения а2 – 4bс, если а = 2, b = 6, с = -10
4. Упростите выражение:
(а - 1)2 (а + 1) + (а + 1)( а - 1)
5. Докажите тождество:
(х - у)2 + (х + у)2 = 2(х2 + у2)
Критерии оценивания
| Отметка | «3» | «4» | «5» |
| Кол- во заданий | 3 задания | 4 задания | 5 заданий |
Контрольная работа №8 по теме «Системы линейных уравнений»
Вариант 2
Решите систему уравнений методом подстановки:

Решите систему уравнений методом сложения:
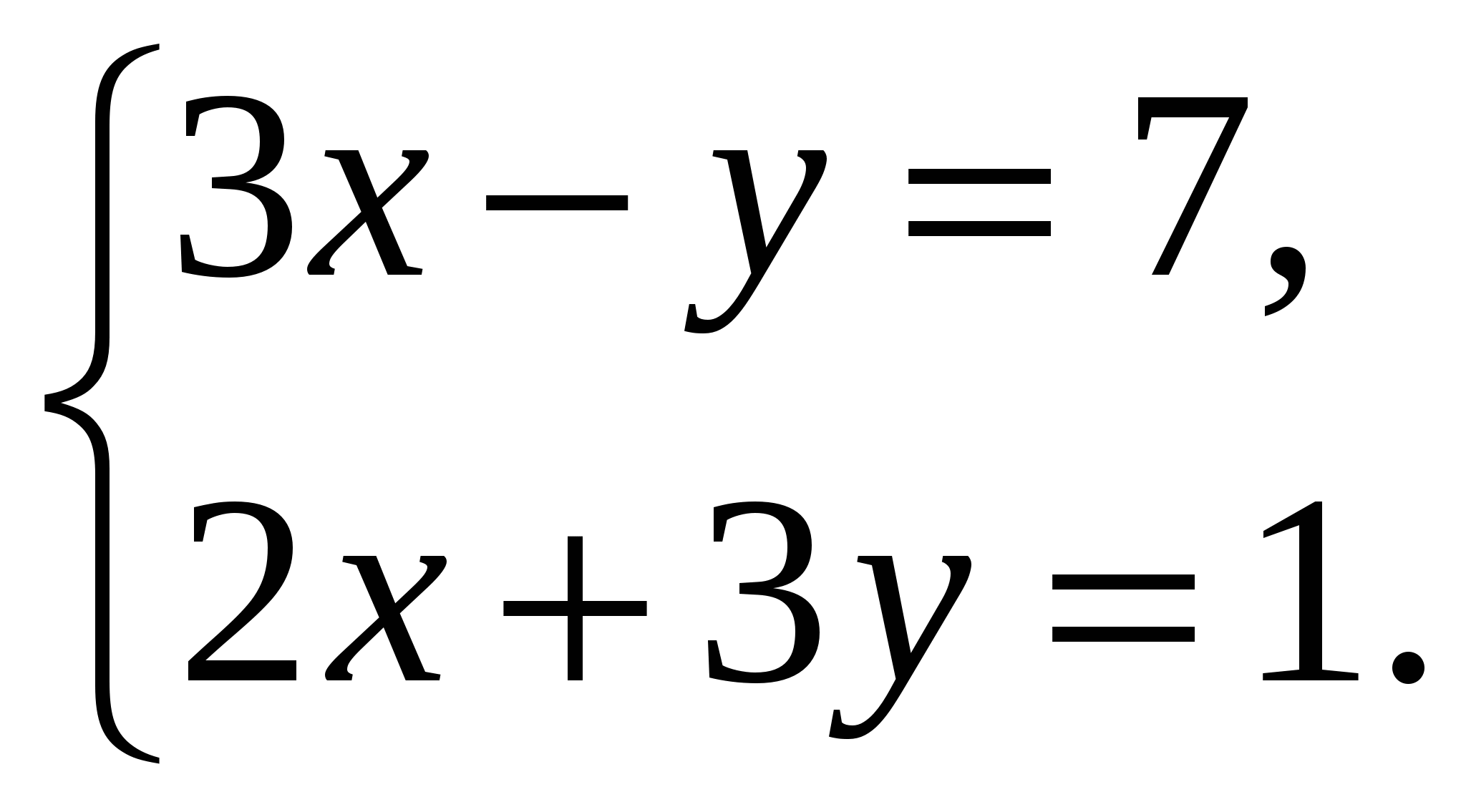
Кассир разменял 500-рублевую купюру на 50-рублевые и 10-рублевые, всего 22 купюры. Сколько было выдано кассиром 50-рублевых и 10-рублевых купюр в отдельности?
Прямая y=kx+b проходит через точки А(5;0) и В(-2;21). Найдите k и b и запишите уравнение этой прямой.
Решите систему уравнений:
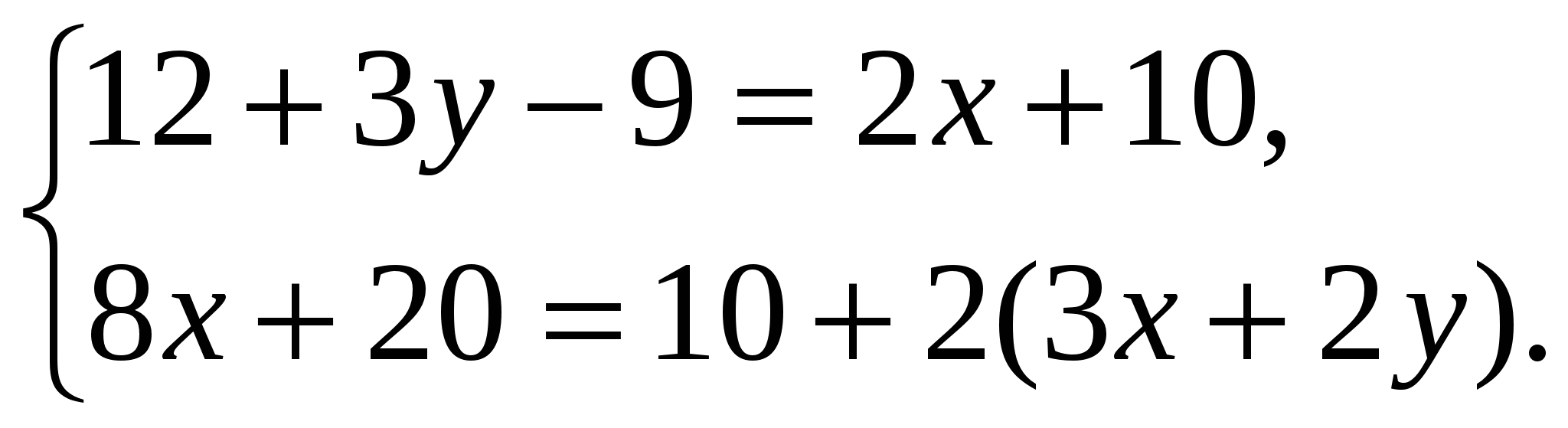
Имеет ли решения система и сколько?

Вариант 1
Решите систему уравнений методом подстановки:
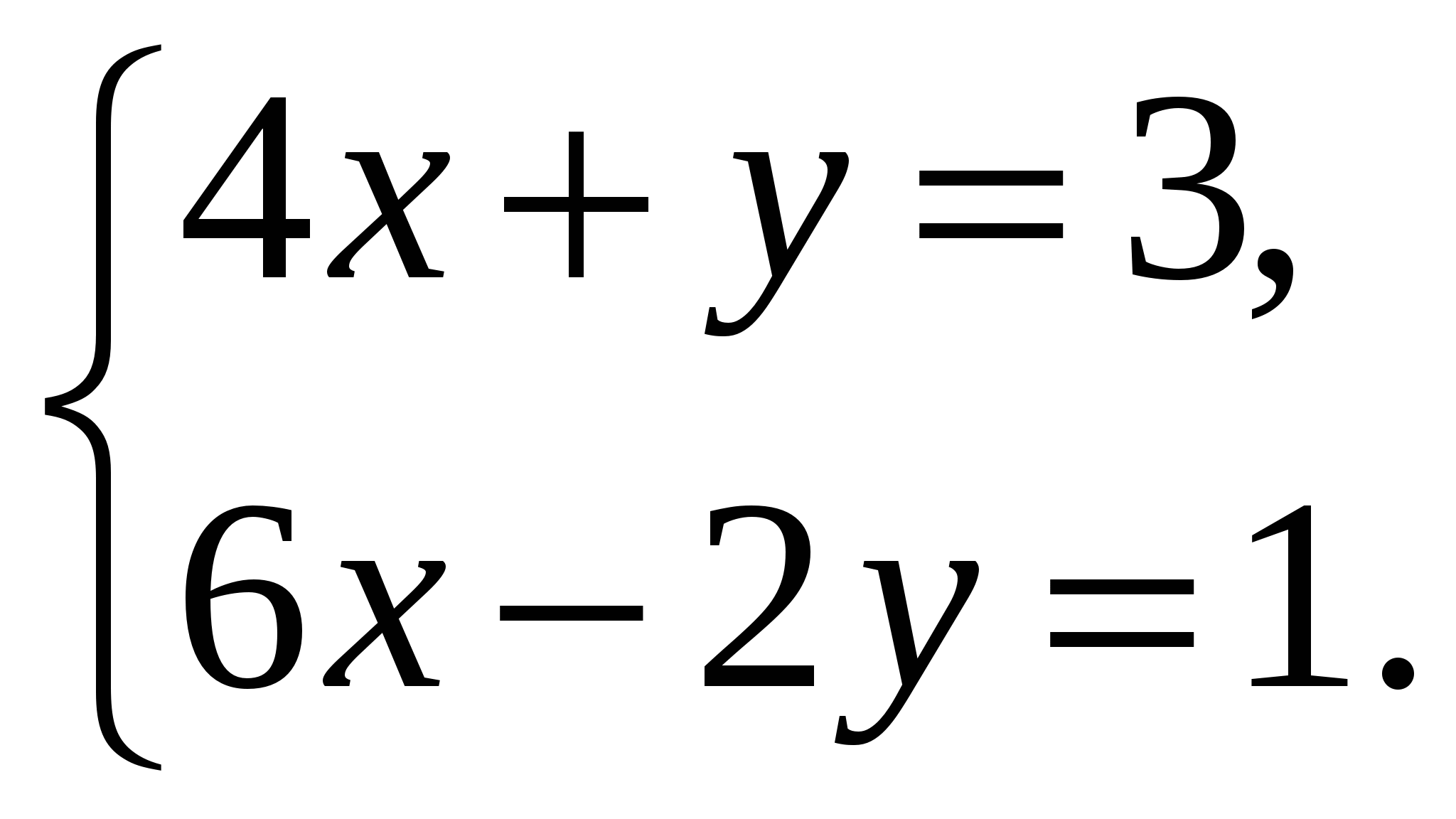
Решите систему уравнений методом сложения:
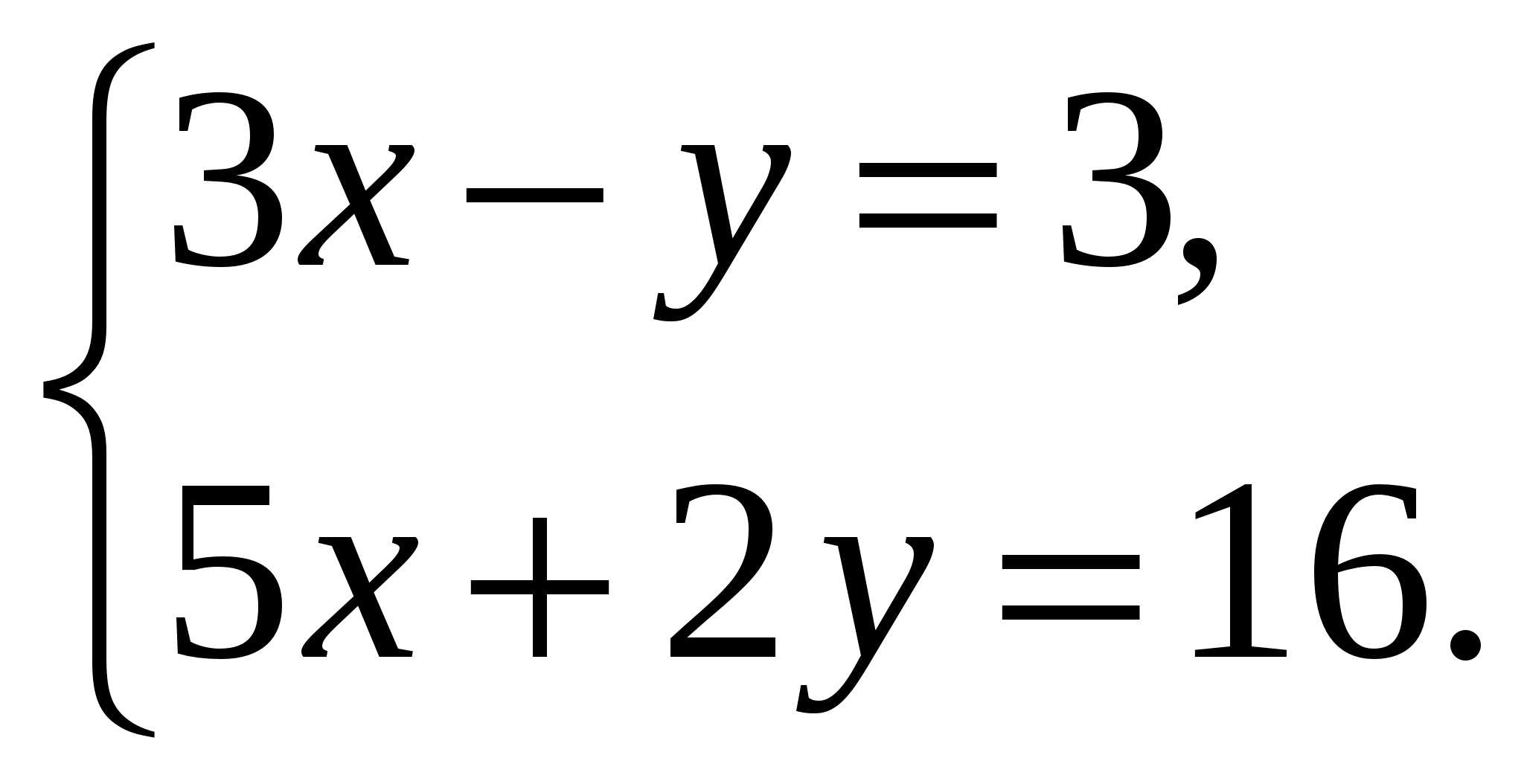
3. Студент получил стипендию 600 руб. купюрами достоинством 50 руб. и 10 руб., всего 24 купюры. Сколько всего было выдано студенту 50-рублевых и 10-рублевых купюр в отдельности?
4. Прямая y=kx+b проходит через точки А(3;8) и В(-4;1). Найдите k и b и запишите уравнение этой прямой.
5. Решите систему уравнений: 
6. Имеет ли решения система и сколько? 
Критерии оценивания
| Отметка | «3» | «4» | «5» |
| Кол- во заданий | 3 задания | 4 задания | 5-6 заданий |
Итоговая контрольная работа
Вариант 1
1. Упростите выражение: ![]()
2. Разложите на множители: ![]()
3. Решите уравнение: ![]()
4. Решите систему уравнений: ![]()
5. Составьте уравнение прямой, проходящей через данные точки: A(1; 7) и В(-1; 3), и постройте ее. Отметьте на построенной прямой точки А и В.
6. Яхта проходит за 10 часов против течения реки такое же расстояние, какое за 8 часов по течению. Найдите скорость течения реки, если собственная скорость яхты равна 18 км/час.
Вариант 2
1. Сократите дробь: ![]()
2. Разложите на множители: 2ху-6у2
3. Решите уравнение: ![]()
4. ![]()
5. Постройте график функции y = 1,5x — 6. Проходит ли график через точку М (-20; 46)?
6. Автомобиль за 3 часа пути проехал на 10 км больше, чем автобус за 4 ч. Найдите скорость автобуса, если она на 20 км/ч меньше скорости автомобиля.
Критерии оценивания
| Отметка | «3» | «4» | «5» |
| Кол- во заданий | 3 задания | 4 задания | 5-6 заданий |


 3504
3504 236
236 ;
; .
. ;
; .
.

 ;
; .
.
 .
. ;
;
 ;
; .
.

 ;
; .
.
 .
.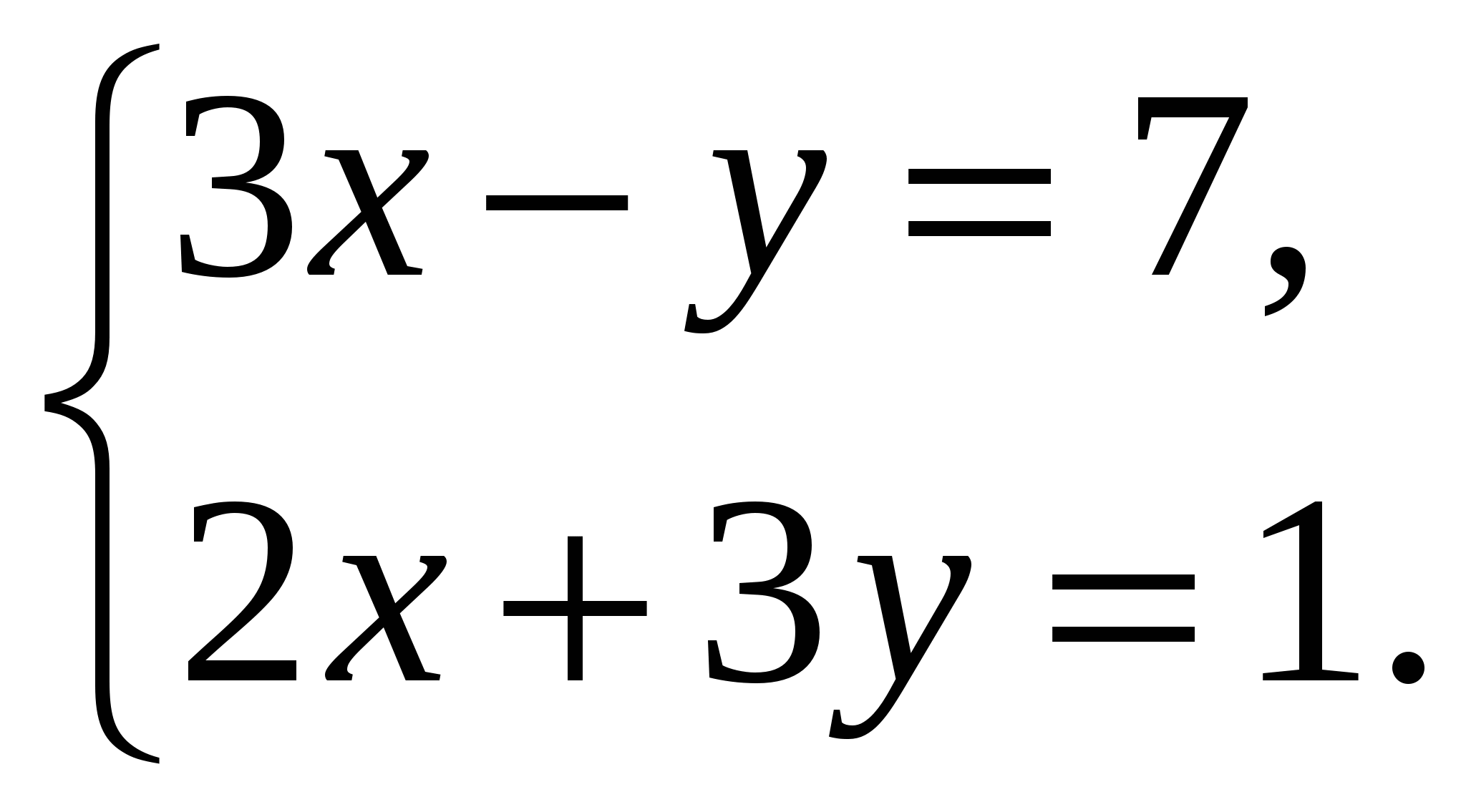
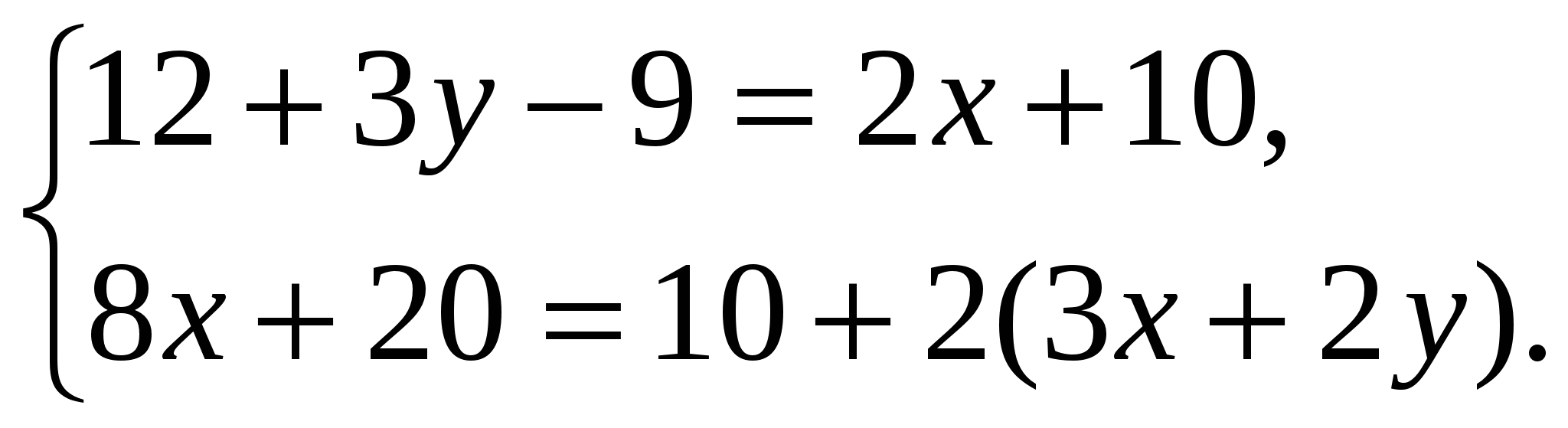
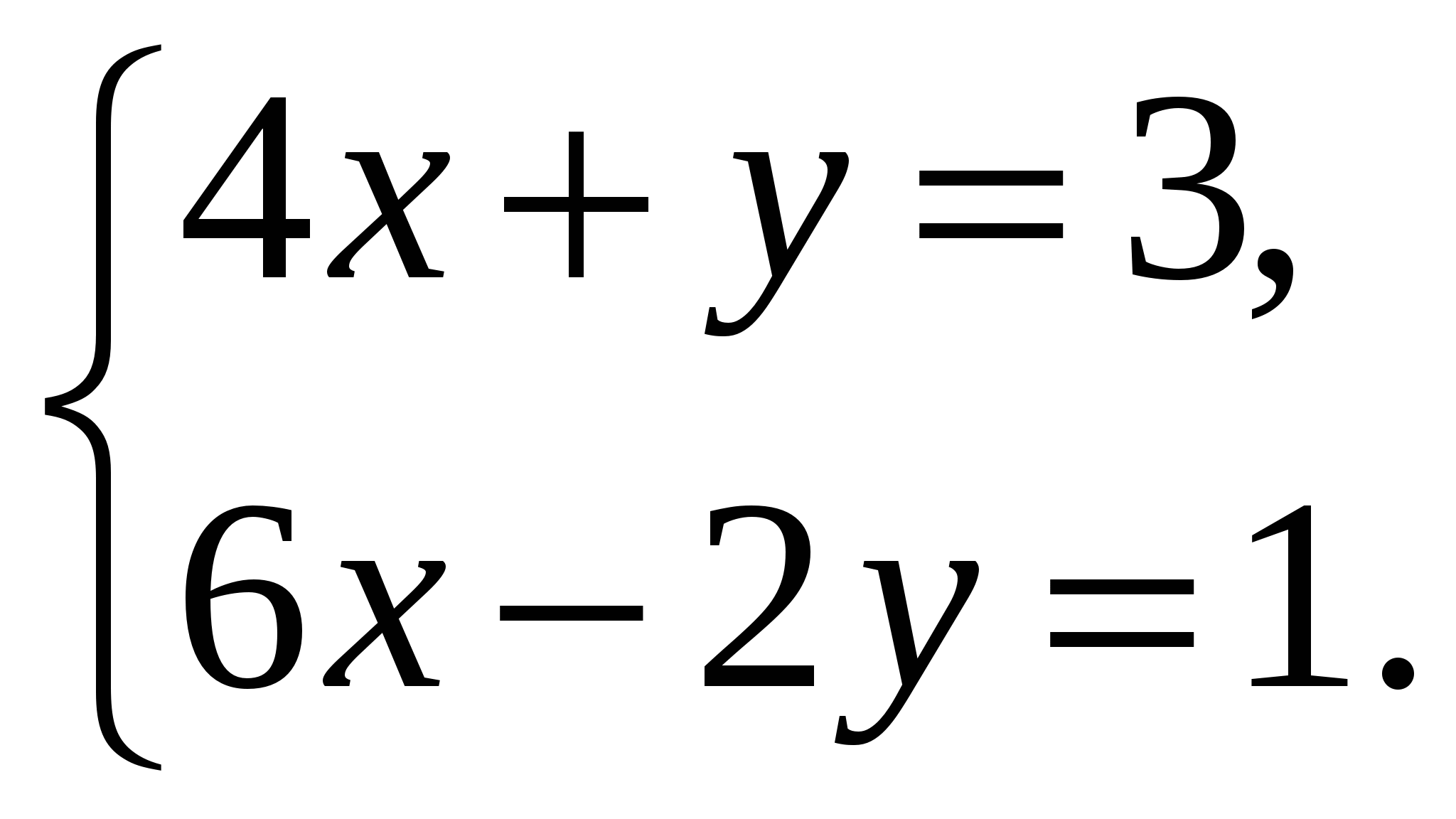
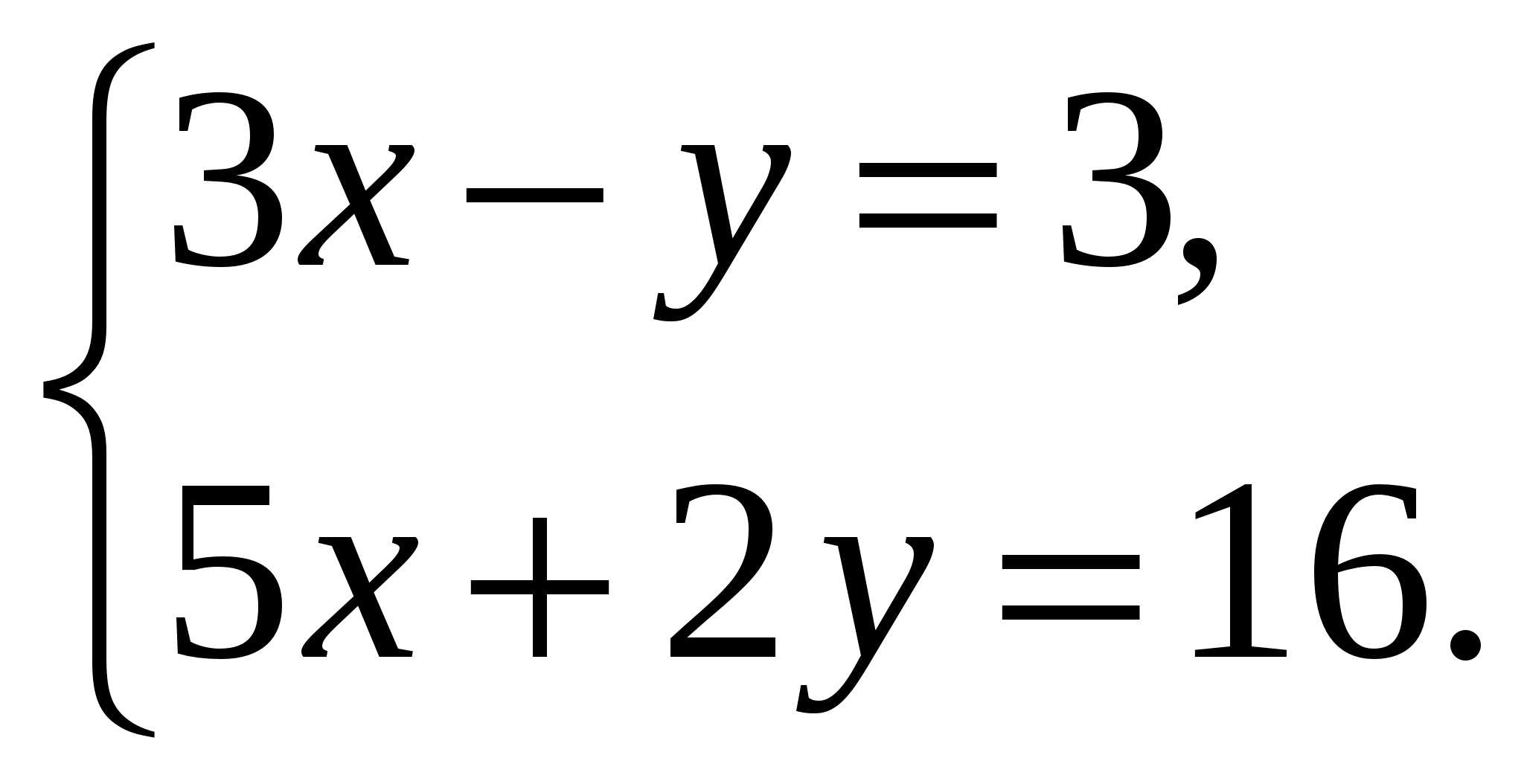
 Рабочая программа по алгебре 7 класс ФГОС
Рабочая программа по алгебре 7 класс ФГОС 