Презентация урока алгебры по теме: "Линейная функция и её график"

Урок-презентация по теме «Линейная функция и её график» (7 класс)

Николаева Евгения Николаевна,

Учитель математики,

г. Шахты

Повтори!!!

• Вопрос №1. Что называют координатной плоскостью ? Ответ.
• Вопрос №2. Что называют функциональной зависимостью ? Ответ.
• Вопрос №3. Какими способами может быть задана функция? Ответ.
• Вопрос №4. Что называют графиком функции ? Ответ.
• Вопрос №5. Что нужно сделать, чтобы построить график функции y = kx ? Ответ.
• Вопрос №6. Что называют прямой пропорциональной зависимостью ? Коэффициентом пропорциональности ? Ответ.

Координатная плоскость -

плоскость на которой выбрана система координат.

Функциональная зависимость -

зависимость

одной переменной

от другой

Способы задания:

функция может быть задана:

формулой,

таблицей,

графиком.

График функции -

- множество всех точек координатной плоскости, абсциссы которых равны значениям независимой переменной, а ординаты – соответствующим значениям функции.

Ответ №5

Для того чтобы построить график функции y = kx , достаточно построить две точки графика, а затем с помощью линейки провести через эти точки прямую.

0 , то зависимость между переменными x и y , выражаемую формулой y = kx , обычно называют прямой пропорциональной зависимостью, а число k - коэффициентом пропорциональности." width="640"

Прямая пропорциональность.

Если значения x , y положительны и k 0 , то зависимость между переменными x и y , выражаемую формулой y = kx , обычно называют прямой пропорциональной зависимостью, а число k - коэффициентом пропорциональности.

Это интересно!!!

Функция - одно из основных математических понятий.

Оно сложилось не сразу. Идея функциональной зависимости началась еще в древности.

В 17 веке большой вклад к появлению понятия функции внесли французские ученые Франсуа Виет и Рене Декарт .

Они разработали единую буквенную математическую символику. Введено было единое обозначение: неизвестных – последними буквами латинского алфавита - x , y , z ,известных – начальными буквами того же алфавита - a , b , c , ... и т. д.

В 1637 году в своей “ Геометрии ” Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы.

Франсуа Виет (1540-1603)

Французский математик. Разработал почти всю элементарную алгебру. Известны «формулы Виета», дающие зависимость между корнями и коэффициентами алгебраического уравнения.

Рене Декарт (1596-1650)

Французский философ, математик, физик и физиолог. Заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввел многие алгебраические обозначения.

В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени.

В 1694 г. слово «функция» ввел впервые Лейбниц (от латинского functio - исполнение, совершение). Под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону.

В 1718 г. известный швейцарский математик Иоганн Бернулли писал: «Функцией переменной величины называется количество, составленное каким угодно способом из этой переменной и постоянных».

Аналогичное определение дал Леонард Эйлер : «Функция переменной величины есть аналитическое выражение, Составленное каким-нибудь способом из этой переменной величины и из чисел, либо из постоянных величин».

Исаак Ньютон (1643-1727)

Английский математик, механик, астроном и физик, создатель классической механики. Фундаментальные труды «Математические начала натуральной философии» (1687) и «Оптика» (1704).

Готфрид Вильгельм Лейбниц (1646-1716)

Немецкий философ, математик, физик, языковед. Он создал основы важного раздела математики – математического анализа. Лейбниц ввел многие понятия и символы, употребляемые в математике и сейчас.

Леонард Эйлер (1707-1783)

Российский ученый - математик, механик, физик и астроном. Ученый необычайной широты интересов и творческой продуктивности. Автор работ по математическому анализу, теории чисел, небесной механике, математической физике, оптике, кораблестроению, теории музыки и других, оказавших значительное влияние на развитие науки.

Изучаем новую тему: «Линейная функция»

Рассмотрим примеры:

Пример 1. На стоянке такси висит табличка:

Обозначим стоимость поездки (в р.) через c , а расстояние (в км) через s . Зависимость стоимости c от расстояния s выражается формулой c=3s+5

Пример 2. В полном баке легкового автомобиля 30 л бензина. На каждый километр пути в среднем расходуется 0,1 л. Количество литров бензина r , которое останется в баке после s км пути, выражается формулой r=30-0,1s

Формулы, которые мы получили, по существу различаются только буквами и числовыми коэффициентами. А по структуре они одинаковы. Таким образом, величины совсем разной природы фактически связаны между собой одной и той же зависимостью. Эти, а также многие другие процессы описываются линейной функцией , которая является их общей математической моделью.

Функция называется линейной , если ее можно задать формулой вида y=kx+b, где k и b - некоторые числа.

Проанализируем разбиение функций на группы в зависимости от значений k и b. (приложение 1.)

Линейная функция – самая простая модель, описания реальных процессов. Так как геометрический образ линейного уравнения y=kx+b на координатной плоскости – это прямая, то графиком линейной функции является прямая.

Немного о функции

0 b k = 1 ; y = x k = -1 ; y = - x K ≠ ±1 ; y = k x b = 0 назад" width="640"

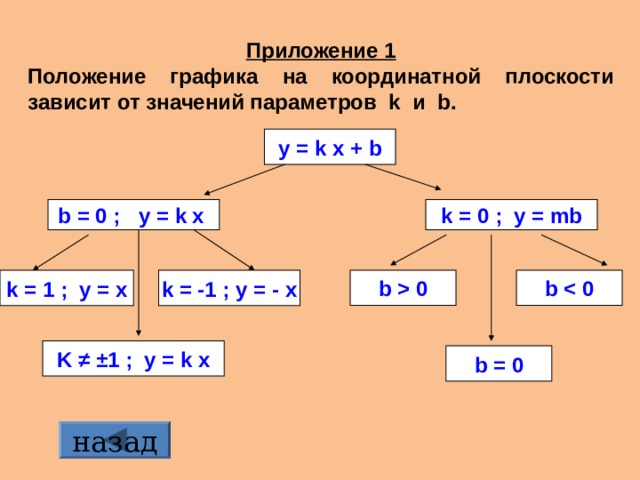
Приложение 1

Положение графика на координатной плоскости зависит от значений параметров k и b .

у = k x + b

b = 0 ; у = k x

k = 0 ; у = mb

b 0

b

k = 1 ; y = x

k = -1 ; y = - x

K ≠ ±1 ; y = k x

b = 0

назад

Стихотворение «Линейная функция».

Пересекаются

При k 1, не равном k 2, Прямые … всегда, А при этом b 1 равно b 2,

Точка пересечения

известна нам тогда.

Прямая

Графиком которой

Является, …

Строгая, красивая, Бесконечная такая.

Совпадут

Если k 1 равно k 2,

Прямые параллельные тогда. А при этом b 1 равно b 2, То прямые … тогда.

Любых.

И каков же тут итог, Если наш учитель строг? Любой ответ по «месту жительства» прямых Найдем мы при условиях …

Линейная

Среди многих функций

Есть одна нужнейшая Важная, старейшая. Зовем ее … ?

1, то угол наклона прямых у = k х к оси 0у больше, чем у графика у = х; если 0 у = х." width="640"

Решаем задачи.

Задача 1.

Построить график функции у=kх, k 0.

При b = 0 линейная функция у = k х + b имеет вид у = k х.

Её график – прямая, проходящая через начало координат. Для построения этой прямой, достаточно задать какую-нибудь одну её точку, отличную от начала координат.

Если k = 1, то функция имеет вид у = х, её график – прямая, являющаяся биссектрисой I и III координатных углов (приложение 2).

Если k = - 1, то функция имеет вид у = - х, её график – прямая, являющаяся биссектрисой II и IV координатных углов (приложение 3).

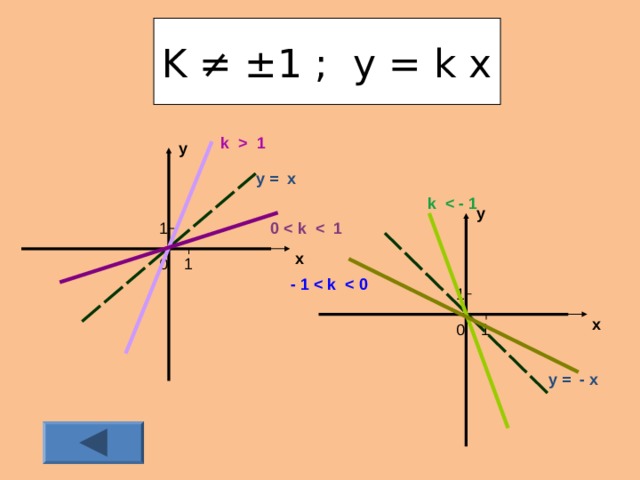
Графики функций у = k х при k ± 1 представлены в (приложении 4).

Если k 1, то угол наклона прямых у = k х к оси 0у больше, чем у графика у = х; если 0

у = х.

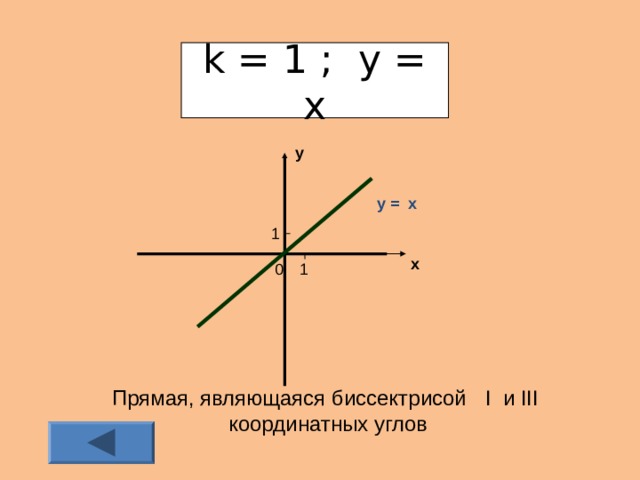
k = 1 ; y = x

у

у = x

1

х

1

0

Прямая, являющаяся биссектрисой I и III координатных углов

Задача 2

Построить график функции у = b.

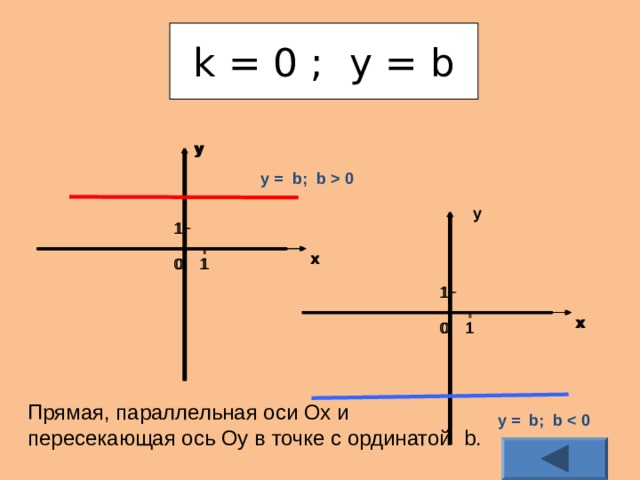
При k = 0 линейная функция у = k х + b имеет вид у = b. Её графиком является прямая, параллельная оси 0х и пересекающая ось 0у в точке с ординатой b (приложение 5).

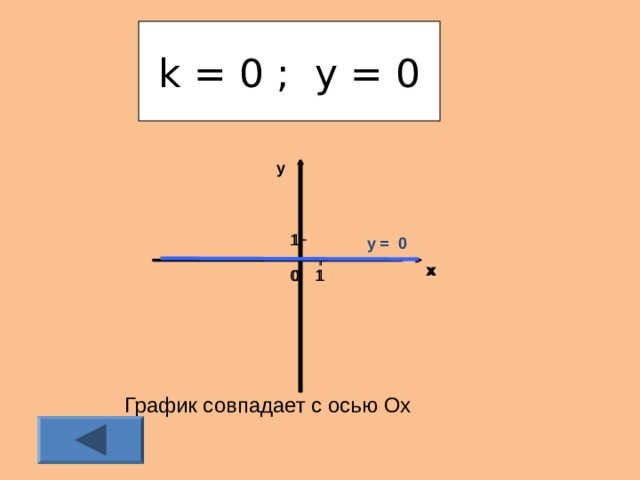
Если не только k = 0, но и b = 0, то функция у = kх имеет вид у = 0. В этом случае её график совпадает с осью Ох (приложение 6).

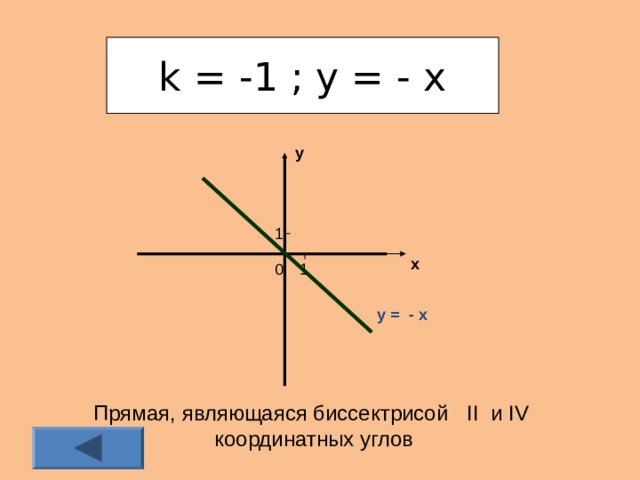
k = -1 ; y = - x

у

1

х

1

0

у = - x

Прямая, являющаяся биссектрисой II и IV координатных углов

1 у у = x k - 1 у 1 0 1 х 1 0 - 1 0 1 х 1 0 у = - x" width="640"

K ≠ ±1 ; y = k x

k 1

у

у = x

k - 1

у

1

0 1

х

1

0

- 1 0

1

х

1

0

у = - x

0 у 1 1 х х 1 0 0 1 1 1 х х 0 1 0 1 Прямая, параллельная оси Ох и пересекающая ось Оу в точке с ординатой b. у = b; b" width="640"

k = 0 ; у = b

у

у

у = b; b 0

у

1

1

х

х

1

0

0

1

1

1

х

х

0

1

0

1

Прямая, параллельная оси Ох и

пересекающая ось Оу в точке с ординатой b.

у = b; b

k = 0 ; у = 0

у

1

1

у = 0

х

х

0

1

1

0

График совпадает с осью Ох

Задачи с ответами

• № 1 Построить график функции y= -3. Ответ
• № 2 Построить график функции y= 0,5 x . Ответ
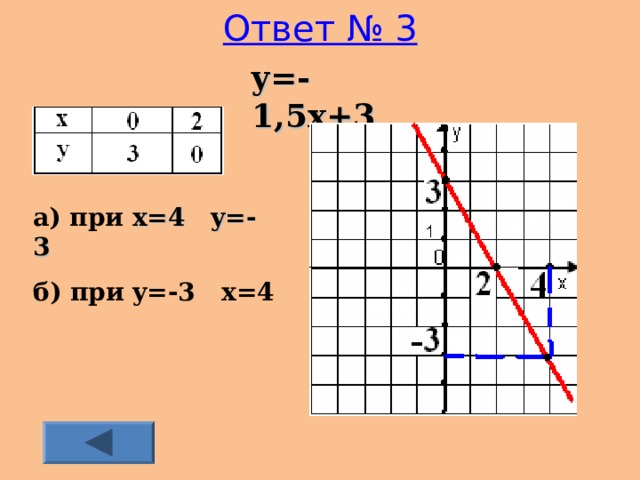
• № 3 Постройте график функции y=-1,5x+3 . Выясните с помощью графика: а) какое значение y соответствует x= 4 ; б) какому значению x соответствует y=- 3 . Ответ
• № 4 Не выполняя построения графика функции y=1,2x-7 , выясните, проходит ли этот график функции через точку А(100;113)? Ответ

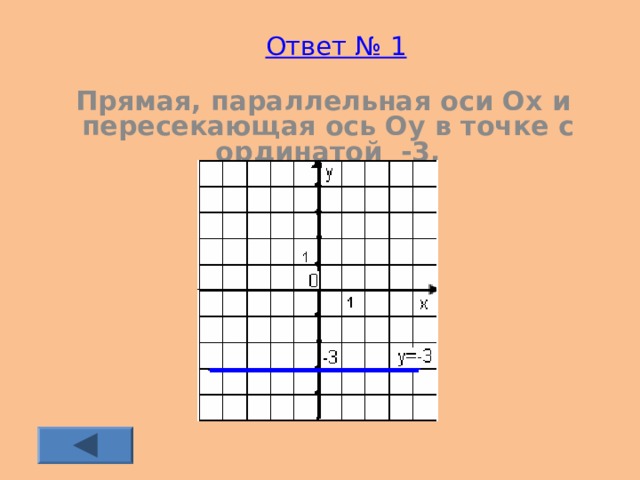
Ответ № 1

Прямая, параллельная оси Ох и пересекающая ось Оу в точке с ординатой -3.

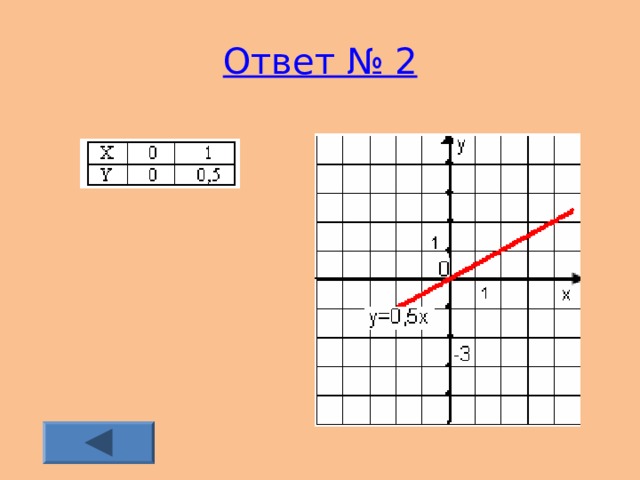
Ответ № 2

Ответ № 3

y=-1,5x+3

а) при x= 4 y=-3

б ) при y=-3 x=4

Ответ № 4

y=1,2x-7 A (100;113), x=100;

Подставляем в функцию y вместо x значение абсциссы точки A : y(x)=x(100)=1,2*100-7=113=y

Ответ: график функции y=1,2x-7 проходит через точку A (100;113) .

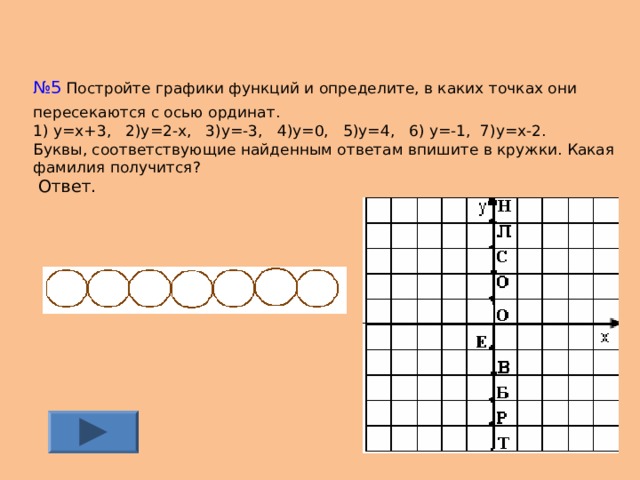
№ 5 Постройте графики функций и определите, в каких точках они пересекаются с осью ординат. 1) y=x+3 , 2)y=2-x , 3)y=-3 , 4)y= 0, 5)y=4 , 6) y=- 1, 7) y=x-2 . Буквы, соответствующие найденным ответам впишите в кружки. Какая фамилия получится? Ответ.

Ответ № 5

Соболев Сергей Львович (1908)

Советский математик, основные труды которого относятся к математическому анализу, математической физике. Большой вклад внес в теорию уравнений.

Задания для работы

• Параграф 32, правила на с. 138-139, №580,
• 581(2,4), 583,
• 584, 586(2), 594(2),
• 595(2), 587(2,4), 607(2,4), 610.

Спасибо за урок!

Желаем успеха в дальнейшем обучении!

Домашнее задание

• Параграф 32, правила на с. 138-139, №581(1,3),
• 582, 585,
• 586(1), 594(1), 595(1).