Пояснительная записка к экзаменационному материалу для промежуточной
аттестации обучающихся 7 классов по математике
Цель проведения промежуточной аттестации – установление соответствия уровня и качества подготовки обучающихся 7-х классов по математике в объеме, установленном обязательным минимумом содержания основного общего образования Государственного образовательного стандарта.
Документы, определяющие содержание контрольно-измерительных материалов:
-Государственный образовательный стандарт (федеральный компонент) основного общего образования (Приказ МО РФ от 05.03.2004. г. № 1089).
Промежуточная аттестация проводится в 7-х классах, изучающих математику на базовом уровне.
На изучение отведено 4 часа в неделю.
Экзаменационный материал для проведения промежуточной аттестации по математике составлен с учётом кодификатора, включающего те элементы содержания из «Обязательного минимума содержания основных образовательных программ», которые изучаются в 7классе основной школы.
Структура работы определяется основными требованиями к уровню подготовки учащихся 7-х классов. Работа содержит 11 заданий. В первую часть включены 8 заданий с выбором одного верного ответа из четырех предложенных или задания с кратким ответом. Во второй части содержится 3 задания с кратким ответом. Задания 1 и 2 частей соответствуют уровню базовой подготовки
На выполнение итогового теста отводится - 60 минут.
Система оценивания выполнения отдельных заданий и работы в целом.
Оценивание работы осуществляется по принципу «сложения», оно зависит от количества и уровня сложности заданий, которые учащийся выполнил верно.
За каждое верно решенное задание первой части учащемуся начисляется 1 балл. Задание первой части считается выполненным верно, если обведена цифра, которая соответствует правильному ответу (в заданиях с выбором ответа), или записан правильный ответ в специально отведенное для этого месте. Задание 10-11 оценивается 2 баллами
Кодификатор
Рациональные дроби
Степень с натуральным показателем
Линейное уравнение
Сложение, вычитание, умножение одночленов и многочленов
Критерии оценивания работы:
| Оценка | Алгебра |
| «5» | Выполнено верно 11-13 заданий |
| «4» | Выполнено верно 10-8 заданий |
| «3» | Выполнено верно 7-6 |
| «2» | Выполнено верно менее 5 заданий |
Вариант 1
Часть А
Модуль «Алгебра»
Найдите значение выражения
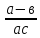 при а = - 4, в = - 6, с = 3
при а = - 4, в = - 6, с = 3
Ответ________________________
Найдите неизвестный член пропорции
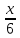 =
= 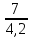
А. 1 Б. 10 B. 0,1 Г. 
Приведите подобные слагаемые в сумме b - 6а- 10b + 9а + 4b
Ответ________________________
Брат в 2 раза старше сестры. Сколько лет сестре и сколько брату, если вместе им 24 года?
Ответ________________________
Упростите выражение 4a3b • (- 3a2b5)
А. 12a5b6 Б. – 7a6b5 B. 1ab-2 Г. - 12a5b6
- 12a5b6
Упростите выражение 3а (а - b) + b (2а - b)
Ответ________________________
7.Решите уравнение (2х + 0,5) = 8х - (3х + 4)
А. - 15 Б. – 1,5 B. 1,5 Г. 15
15
8.Разложите на множители 9y2 – 25
Ответ________________________
9.Лодка сначала плыла 4 ч по озеру, а потом 5 ч по реке против ее течения. За это время она проплыла 30 км. Скорость течения реки 3 км/ч. Найдите собственную скорость лодки.
Пусть х км/ч — собственная скорость лодки. Какое уравнение соответствует условию задачи?
А. 4х + 5 (х + 3) = 30. Б. 4х + 5х - 3 = 30.
B. 4х + 5 (х - 3) = 30. Г.  +
+  = 30.
= 30.
10.а) Постройте график функции у = 2х + 2.
б) Определите, проходит ли график функции через точку А(- 10; - 18).
11.Вычислите
а)  ; б)
; б) 
Вариант 2
Часть А
Модуль «Алгебра»
1.Найдите значение выражения  при а = - 5, в = 6, с = 7
при а = - 5, в = 6, с = 7
Ответ________________________
2.Найдите неизвестный член пропорции  =
= 
А. 1 Б. 5 B. 0,5 Г. 35
3.Приведите подобные слагаемые в сумме а - 7в + 3а - 4а - 6в
Ответ________________________
4.В двух вагонах поезда 86 человек, причем в первом на 14 человек меньше, чем во втором. Сколько человек в каждом вагоне?
Ответ________________________
5.Упростите выражение 4a7b5 • (- 2ab2)
А. 2a6b3 Б. – 8a8b7 B. 6a7 b3 Г. 8a8b7
8a8b7
6.Упростите выражение 2х (3х - 4) – 3х (3х - 1)
Ответ________________________
7.Решите уравнение 5х + 3 = 7х – 5 (2х + 1)
А. 8 Б. – 1 B. 0 Г. 1
1
8. Разложите на множители 16y2 – 81
А. (16y-9)(16y+9) Б. (4y-9)(4y+9) B. (16y-81)(16y+81) Г. (4y-9)(4y-9)
(4y-9)(4y-9)
9.Автомобиль и автобус, находящиеся на расстоянии 30 км друг от друга, одновременно начали движение навстречу друг другу. Они встретились через полчаса. Скорость автомобиля в полтора раза больше скорости автобуса. Какова скорость автобуса?
Пусть х км/ч — скорость автобуса. Какое уравнение соответствует условию задачи?
А. 0,5 (1,5х - х) = 30. Б. х + 1,5х . 0,5 = 30.
B. 0,5 (1.5 +х) + 0,5х = 30. Г. 0.5х + 0,5 . 1,5х = 30.
10. а) Постройте график функции у = - 2х - 2.
б) Определите, проходит ли график функции через точку А(10; - 20).
11. а)  ; б)
; б)


 6002
6002 402
402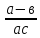 при а = - 4, в = - 6, с = 3
при а = - 4, в = - 6, с = 3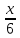 =
= 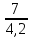
 Итоговая контрольная работа по алгебре 7кл Макарычев
Итоговая контрольная работа по алгебре 7кл Макарычев 