Внеурочная работа преподавателя математики ( роль конкурсов и КВН в обучении)

Внеурочная работа преподавателя математики

( роль конкурсов и КВН в обучении)

Рогачев В.В., преподаватель математики

Что сделать для того, чтобы для студентов математика стала любимым предметом? Кроме того, чтобы разнообразить методы проведения уроков, я считаю необходимым проводить математические веселые минутки и КВН, в которых для решения задач надо применять логику, смекалку. Кроме того, такие мероприятия учат работе в коллективе, вырабатывают дух соперничества, стимулируют активную познавательную деятельность. Конкурсы должны быть веселые, с разным уровнем сложности, интересны по содержанию.

Сейчас время интернет-технологий, поэтому кабинеты оснащены выходом в интернет, что помогает в считанные минуты найти интересные задачки и головоломки для тех ребят, которые на перемене просто сидят в классе или неотрывно пользуются телефонами. Мои студенты сразу, приходя в кабинет, спрашивают такие задания, которые требуют быстрого решения, интересны и поучительны. Например, математические софизмы. Это умышленно ложное умозаключение, которое имеет видимость правильного. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в математических софизмах выполняются «запрещённые» действия или не учитываются условия применимости теорем, формул и правил. Иногда рассуждения ведутся с использованием ошибочного чертежа или опираются на приводящие к ошибочным заключениям «очевидности». Встречаются софизмы, содержащие и другие ошибки.

Чем же полезны софизмы для изучающих математику? Что они могут дать? Разбор софизмов, прежде всего, развивает логическое мышление, то есть прививает навыки правильного мышления. Обнаружить ошибку в софизме – это значит осознать её, а осознание ошибки предупреждает от повторения её в других математических рассуждениях. Разбор софизмов помогает сознательному усвоению изучаемого математического материала, развивает наблюдательность, вдумчивость и критическое отношение к тому, что изучается.

Вот такие софизмы я нашел в интернет-ресурсах.

Попробуй свои силы:

1) 4 р.= 40 000 к. Возьмем верное равенство: 2р.=200 к. Возведём его по частям в квадрат. Мы получим: 4 р.=40 000 к. В чём ошибка?

2) 5=6. Попытаемся доказать, что 5=6. С этой целью возьмем числовое тождество:

35+10-45=42+12-54. Вынесем общие множители левой и правой частей за скобки. Получим: 5(7+2-9)=6(7+2-9). Разделим обе части этого равенства на общий множитель (заключённый в скобки). Получаем 5=6. В чём ошибка?

3). 2*2=5. Найдите ошибку в следующих рассуждениях. Имеем верное числовое равенство: 4:4=5:5. Вынесем за скобки в каждой части его общий множитель. Получим: 4(1:1)=5(1:1). Числа в скобках равны, поэтому 4=5, или 2*2=5.

4) Все числа между собой равны. Пусть m=n. Возьмем тождество: m²-2mn+n²=n²-2mn+m². Имеем: (m-n)²=(n-m)². Отсюда m-n=n-m? или 2m=2n, а значит, m=n. В чём ошибка?

В другом источнике я нашел такие задачки:

• Как записать в общем виде натуральное число, при делении которого на 5 получается остаток 7?

• Найдите наименьшее значение выражения 4x²-2x+10.

• Самолёт из Москвы летит в Киев и возвращается обратно в Москву. В какую погоду этот самолёт проделает весь путь быстрее: в безветренную; при ветре, дующем с одинаковой силой в направлении Москва-Киев?

• Из разговора 1 сентября: «Сколько тебе ещё учиться?» - «Столько, сколько ты уже проучился. А тебе?» - «В полтора раза больше». Кто в какой класс перешёл?

• В записи КТС+КСТ=ТСК каждой букве соответствует своя цифра. Найдите, чему равно число ТСК!

ДОКАЖИТЕ!

• Квадрат нечётного числа – нечётное число.

• Квадрат чётного числа является числом, кратным 4.

• Разность квадратов двух последовательных нечётных чисел делиться на 8.

• Сумма произведения двух последовательных натуральных чисел и большего из них равна квадрату этого большего числа.

• Если взять какое-нибудь двузначное число с разными цифрами, переставить в нём цифры и вычесть из взятого числа получившееся, то разность будет делиться на 9. Будет ли это верно для трехзначных чисел (переставляются крайние цифры)?

Немало в интернете и задач-головоломок по геометрии

Спираль Архимеда. Представьте себе, что по радиусу равномерно вращающегося диска с постоянной скоростью ползёт муха. Путь, описанный мухой, - это кривая, называемая спиралью Архимеда. Начертите какую-нибудь спираль Архимеда.

Синусоида. Сделайте из плотной бумаги, свернув её несколько раз, трубочку. Разрежьте эту трубочку наклонно. Смотрите на линию разреза, если развернуть одну из частей этой трубочки. Перерисуйте эту линию на лист бумаги. У вас получится одна из замечательных кривых, называемая синусоидой. Особенно часто с ней приходится встречаться при изучении электротехники и радиотехники.

Кардиоида. Возьмите два равных кружочка, вырезанных из фанеры (можно взять две одинаковые монеты). Один из этих кружочков закрепите. Второй приложите к первому, отметьте на краю его точку А, наиболее удалённую от центра первого кружка. Затем катите без скольжения подвижный кружочек по неподвижному и наблюдайте, какую линию опишет точка А. Начертите эту линию. Она является одной из улиток Паскаля и называется кардиоидой. В технике эта кривая часто используется для устройства кулачковых механизмов.

Геометрические головоломки очень интересны ребятам

• Сложите три равных квадрата: 1) из 11 спичек; 2) из 10 спичек.

• Постройте замкнутую ломаную линию, состоящую из трёх звеньев и проходящую через четыре данные точки.

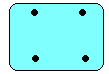
• Как разместить 6 кружков на плоскости так, чтобы получились 3 ряда по 3 кружка и 6 рядов по 2кружка.

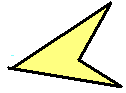
• Изображённую на рисунке фигуру требуется разделить на 6 частей, проведя всего лишь 2 прямые. Как это сделать?