Система задач по теме
«Дифференциальные уравнения»
для 11 классов физико-математического профиля
Дифференциальные уравнения - одна из самых сложных тем школьного курса математического анализа. Изучение этой темы имеет большое образовательное и прикладное значение. Дифференциальные уравнения помогают моделировать различные процессы и задачи из многих областей естествознания, демонстрируют необходимость математических знаний для людей самых разных профессий.
Математика практически единственный учебный предмет, в котором задачи используются и как цель, и как средство обучения, а иногда и как предмет изучения. Ограниченность учителя временными рамками урока и временем изучения темы, нацеленность учителя и учащихся на достижение ближайших целей – все это никак не способствует решению на уроке большого количества задач, задач творческого характера, нестандартных задач, задач повышенного уровня сложности, задач, при решении которых необходимы знания разделов математики, выходящих за пределы школьного курса. Предлагаемая система задач позволяет систематизировать и расширить знания учащихся в решении дифференциальных уравнений.
Среди заданных соотношений выделите дифференциальные уравнения. Объясните, почему остальные соотношения не относятся к дифференциальным уравнениям:










Соотношения вида
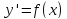 можно считать простейшими дифференциальными уравнениями. Найдите множество решений уравнения:
можно считать простейшими дифференциальными уравнениями. Найдите множество решений уравнения:





Являются ли данные функции решениями дифференциального уравнения? Если да, то попытайтесь подобрать еще несколько его решений (подсказка: попробуйте подставить функции
 ).
).
| Дифференциальные уравнения | Частные решения | Дидактические функции задачи |
|
|
|
|
Дано дифференциальное уравнение
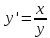 .
. Запишем уравнение в виде:
 .
.
Найдите первообразные для левой и правой частей уравнения.
Верно ли, что найденные первообразные совпадают? Если нет, то насколько сильно они могут различаться?
Запишите соотношение между переменными
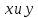 , которое следует из дифференциального уравнения. Выразите
, которое следует из дифференциального уравнения. Выразите 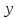 через
через 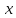 .
. Есть ли у дифференциального уравнения другие решения, кроме найденных?
Среди уравнений задачи 2 найдите:
Линейные однородные дифференциальные уравнения первого рода.
Линейные неоднородные дифференциальные уравнения первого порядка; запишите соответствующие им линейные однородные дифференциальные уравнения.
Сформулируйте гипотезу об общем решении линейного однородного дифференциального уравнения. Какую часть этой гипотезы вы можете доказать? Сравните решения неоднородного дифференциального уравнения с решениями соответствующего однородного дифференциального уравнения.
Сформулируйте гипотезу об общем решении линейного неоднородного дифференциального уравнения. Сможете ли вы доказать эту гипотезу?
Докажите, что решениями уравнения
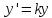 (
(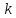 – некоторое действительное число) являются функции
– некоторое действительное число) являются функции 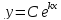 .
.Запишем уравнение в виде
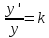 . Проверьте, что функция
. Проверьте, что функция 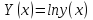 является первообразной для функции
является первообразной для функции 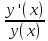 . Найдите все первообразные постоянной функции
. Найдите все первообразные постоянной функции 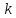 . Сделайте вывод.
. Сделайте вывод.Из полученного равенства выразите
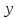 как функцию от
как функцию от 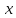 .
.
Дано дифференциальное уравнение
Можно ли найти первообразные для левой и правой частей уравнения?
Представьте уравнение в виде, удобном для интегрирования.
Проинтегрируйте обе части уравнения, получите семейство его решений. Все ли решения найдены?
К каким из дифференциальных уравнений задачи 2 можно применить указанный метод («разделение переменных»)? Найдите общее решение этих уравнений.
Найдите частное решение дифференциального уравнения
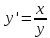 , удовлетворяющее условию
, удовлетворяющее условию .
Даны дифференциальные уравнения:
,
,
,
,
,
,
,
,
. Среди заданных дифференциальных уравнений найдите:
Линейные однородные дифференциальные уравнения второго порядка.
Линейные неоднородные дифференциальные уравнения второго порядка; запишите соответствующие им линейные однородные дифференциальные уравнения.
Нелинейные дифференциальные уравнения второго порядка.
Запишите еще несколько линейных однородных дифференциальных уравнений второго порядка.
Для каждого из дифференциальных уравнений п. 9.1, 9.4 подберите решения вида некоторое число. Сколько таких решений получится в каждом случае?
Как вы думаете, какой вид имеет общее решение однородного линейного дифференциального уравнения второго порядка? Какую часть гипотезы вы можете доказать?
Найдите частное решение (с заданным начальным условием) для дифференциального уравнения первого порядка:
a);
;
b) ;
;
c) ;
.
Постройте эскизы графиков найденных решений (интегральные кривые уравнения). Сделайте выводы.
Сколько начальных условий нужно задать для нахождения частного решения дифференциального уравнения второго порядка?
Найдите частные решения следующих дифференциальных уравнений:
дифференциального уравнения
с начальными условиями:
a) ;
b)
дифференциального уравнения
с начальными условиями:
a)
b)
дифференциального уравнения
с начальными условиями:
a)
b)
Как ведут себя найденные решения при
?
Стационарное (постоянное) решение
, i=1, 2, …, n дифференциального уравнения называется устойчивым по Ляпунову при t , если для любого 0 существует такое 0, зависящее от и t0, что любое решение
, для которого при t=t0 выполняется неравенство:
|
| |
удовлетворяет неравенству
| | |
для всех i = 1, 2, …, n.
Решение , i=1, 2, …, n, называется неустойчивым, если существует 0 такое, что для любого 0 найдется такой момент времени t=t1, что для некоторого значения i=k будет выполняться неравенство
|
| |
несмотря на то, что для всех i=1, 2, …, n.
Решение называется асимптотически устойчивым, если:
решение
устойчиво по Ляпунову при t ;
существует такое число H0, что для любого решения
, удовлетворяющего при t=t0 неравенству ), i=1, 2, …, n, будет справедливо равенство
|
|
|
Является ли устойчивым решение
в задачах 11.1-11.3?
Сможете ли вы, не решая уравнения, предположить, будет ли его решение
устойчивым?
Можно доказать, что нулевое решение устойчиво, если в общем решении
все множители
, … ,
; неустойчиво, если в общем решении
хотя бы один из множителей
, … ,
. Проверьте справедливость этих признаков на примере задач 11.1-11.3.
Исходя из определения устойчивости по Ляпунову, выясните, устойчивы ли решения данных уравнений с указанными начальными условиями:
Исследуйте на устойчивость решения системы уравнений
. Изобразите траектории решений и укажите направление движения по траекториям.
Исследуйте на устойчивость решения системы уравнений
. Изобразите траектории решений этой системы и укажите направление движения по траекториям.
При каких действительных
и
действительные части корней многочлена отрицательны?
Найдите все действительные значения параметров
, при которых решения системы уравнений
асимптотически устойчивы.
Определите тип положения равновесия и характер поведения фазовых кривых системы уравнений
. Сделайте чертеж.
Постройте фазовые кривые системы уравнений в зависимости от значений параметра
(рассмотрите случаи
).


 967
967 18
18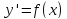 можно считать простейшими дифференциальными уравнениями. Найдите множество решений уравнения:
можно считать простейшими дифференциальными уравнениями. Найдите множество решений уравнения: ).
). 

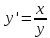

















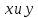 , которое следует из дифференциального уравнения. Выразите
, которое следует из дифференциального уравнения. Выразите 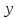 через
через 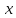 .
. 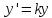 (
(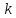 – некоторое действительное число) являются функции
– некоторое действительное число) являются функции 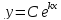 .
.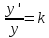 . Проверьте, что функция
. Проверьте, что функция 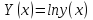 является первообразной для функции
является первообразной для функции 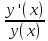 . Найдите все первообразные постоянной функции
. Найдите все первообразные постоянной функции  Система задач по теме «Дифференциальные уравнения» для 11 классов физико-математического профиля
Система задач по теме «Дифференциальные уравнения» для 11 классов физико-математического профиля 