Пособие для подготовки к ОГЭ по математике (9 класс)

Литература по подготовке к ОГЭ по математике

1. ОГЭ 2018. Математика.  Основной государственный экзамен. 50 вариантов типовых тестовых  заданий/ И.Р. Высоцкий, Л.О. Рослова, Л.В. Кузнецова под ред. И.В. Ященко. – М.: Издательство «Экзамен», 2017 -295.

2. ОГЭ 2018. Математика: тематические тренировочные задания:9 класс/ В.В. Кочагин, М.Н. Кочагина. – Москва: Эксмо, 2017. – 192с. – ( ОГЭ. Тематические тренировочные задания)

3. Используются сайты http://fipi.ru/ и https://oge.sdamgia.ru (Решу ОГЭ), neznaika.pro,  maximumtest.ru

4. ОГЭ. Математика. Задачник. Сборник заданий и методических рекомендаций/ Ю.А. Глазков, М.Я.Гаиашвили. – М.: Издательство «Экзамен», 2017. -367,[1] с.

5.Статград

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №1

сельского поселения «Село Пивань».

Пособие для

итогового повторения курса

математики 7-9х классов.

Автор: учитель математики и информатики

Гужавина Л.С.

2017/2018 учебный год

Пояснительная записка.

Программа курса позволяет осуществить подготовку к государственной итоговой аттестации по математике в 9 классе. Изучая курс, учащиеся познакомятся со всеми типами заданий, со всеми идеями и методами их решений. На занятиях рассматриваются наиболее ценные, содержательные и поучительные задачи, проверяющие не только подготовку учащихся, но и их умение мыслить в нестандартной ситуации.

Данная программа составлена на основе обязательного минимума содержания основного общего образования по математике. Основная методическая линия курса – организация самостоятельной работы учащихся, при направляющей роли учителя.

Методика преподавания данного курса предполагает уровневую дифференциацию, которая задает различную глубину освоения фиксированного содержания и достижения различных уровней планируемых результатов обучения.

Цели и задачи проведения курса.

1. Формирование у всех учащихся базовой математической подготовки, составляющей функциональную основу общего образования.

2. Создание для части школьников условий, способствующих получению повышенного уровня подготовки, достаточной для активного использования математики в дальнейшем обучении, прежде всего при изучении ее в старших классах на профильном уровне.

Требования к уровню подготовки учащихся.

1. В результате изучения содержания курса учащиеся должны знать:

• Простейшие задачи, элементарные составляющие, из которых складываются более сложные задачи;

• Глобальные методы решения математических задач;

1. В процессе обучения учащиеся приобретают следующие умения:

• Выделять типы задач;

• Определять методы решения задачи;

• Отбирать оптимальный метод, который будет использоваться при решении задачи;

• Самостоятельно получать и применять знания.

Диагностическая работа №5

1.

Четырёхугольник ABCD впи­сан в окружность. Угол ABD равен 85°, угол CAD равен 19°. Най­ди­те угол ABC. Ответ дайте в градусах.

2.

Два катета прямоугольного треугольника равны 20 и 21. Найдите гипотенузу этого треугольника.

3.

Отрезок AB = 40 ка­са­ет­ся окруж­но­сти ра­ди­у­са 75 с цен­тром O в точке B. Окруж­ность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­ди­те AD.

4.

Прямоугольный тре­уголь­ник с ка­те­та­ми 5 см и 12 см впи­сан в окружность. Чему равен ра­ди­ус этой окружности?

5. Найдите пло­щадь кругового сектора, если длина огра­ни­чи­ва­ю­щей его дуги равна 6π, а угол сек­то­ра равен 120°. В от­ве­те укажите площадь, деленную на π.

6. Сторона квад­ра­та равна 10. Най­ди­те его площадь.

7.

На ри­сун­ке изображена тра­пе­ция  . Ис­поль­зуя рисунок, най­ди­те .

8.

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

9. Какое из следующих утверждений верно?

1. Все углы ромба равны.

2. Вписанный угол, опирающийся на диаметр окружности, прямой.

3. Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.

В ответ запишите номер выбранного утверждения.

10. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Каж­дая сто­ро­на тре­уголь­ни­ка мень­ше раз­но­сти двух дру­гих сторон.

2) В рав­но­бед­рен­ном тре­уголь­ни­ке име­ет­ся не более двух рав­ных углов.

3) Если сто­ро­на и угол од­но­го тре­уголь­ни­ка со­от­вет­ствен­но равны сто­ро­не и углу дру­го­го треугольника, то такие тре­уголь­ни­ки равны.

4) В тре­уголь­ни­ке ABC, для ко­то­ро­го AB = 3, BC = 4, AC = 5, угол C наименьший.

Диагностическая работа №6

1. Для фрук­то­во­го на­пит­ка сме­ши­ва­ют яб­лоч­ный и ви­но­град­ный сок в от­но­ше­нии 13:7. Какой про­цент в этом на­пит­ке со­став­ля­ет ви­но­град­ный сок?

2. Поезд, дви­га­ясь рав­но­мер­но со ско­ро­стью 150 км/ч, про­ез­жа­ет мимо стол­ба за 18 се­кунд. Най­ди­те длину по­ез­да в мет­рах.

3. Товар на рас­про­да­же уце­ни­ли на 20%, при этом он стал сто­ить 680 р. Сколь­ко стоил товар до распродажи?

4. Средний рост жителя города, в котором живет Никита, равен 169 см. Рост Никиты 183 см. Какое из следующих утверждений верно?

1. Обязательно найдется житель с ростом менее 170 см.

2. Все жители города, кроме Никиты, имеют рост меньше 169 см.

3. Все жители города ниже Никиты.

4. Обязательно найдется житель города с ростом 158 см.

5. Для эк­за­ме­на под­го­то­ви­ли би­ле­ты с но­ме­ра­ми от 1 до 50. Ка­ко­ва ве­ро­ят­ность того, что на­у­гад взя­тый уче­ни­ком билет имеет од­но­знач­ный номер?

6. На эк­за­ме­не по био­ло­гии школь­ни­ку достаётся один слу­чай­но вы­бран­ный во­прос из списка. Ве­ро­ят­ность того, что этот во­прос на тему «Членистоногие», равна 0,15. Ве­ро­ят­ность того, что это ока­жет­ся во­прос на тему «Ботаника», равна 0,45. В спис­ке нет вопросов, ко­то­рые од­но­вре­мен­но от­но­сят­ся к этим двум темам. Най­ди­те ве­ро­ят­ность того, что на эк­за­ме­не школь­ни­ку до­ста­нет­ся во­прос по одной из этих двух тем.

7. Площадь па­рал­ле­ло­грам­ма  можно вы­чис­лить по фор­му­ле , где  — сто­ро­ны параллелограмма (в метрах). Поль­зу­ясь этой формулой, най­ди­те площадь параллелограмма, если его сто­ро­ны 10 м и 12 м и .

8. Площадь четырёхугольника можно вы­чис­лить по фор­му­ле  где d₁ и d₂ — длины диа­го­на­лей четырёхугольника, α — угол между диагоналями. Поль­зу­ясь этой формулой, най­ди­те длину диа­го­на­ли d₁, если  а 

9. Зная длину сво­е­го шага, че­ло­век может приближённо под­счи­тать пройденное им рас­сто­я­ние s по фор­му­ле s = nl, где n — число шагов, l — длина шага. Какое рас­сто­я­ние прошёл человек, если l = 80 см, n = 1600? Ответ вы­ра­зи­те в километрах.

Тренировочный вариант №1

1. Найдите зна­че­ние вы­ра­же­ния  

2.

Завуч школы под­вел итоги по вы­бо­ру предметов для сдачи ЕГЭ уча­щи­ми­ся 11-х классов. Ре­зуль­та­ты представлены на диаграмме. Сколь­ко примерно уча­щих­ся выбрали для сдачи ЕГЭ физику?

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1) 16

2) 12

3) 14

4) 8

3. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число  Рас­по­ло­жи­те в по­ряд­ке убы­ва­ния числа   и 

В от­ве­те укажите номер пра­виль­но­го варианта.

1) 

2) 

3) 

4) 

4. Какое из данных ниже чисел является значением выражения 

1) 16

2) 

3) −16

4) 

5. На диа­грам­ме пред­став­ле­ны не­ко­то­рые из круп­ней­ших по чис­лен­но­сти на­се­ле­ния стран мира.

Чис­лен­ность на­се­ле­ния ка­ко­го го­су­дар­ства при­мер­но в 6 раз мень­ше чис­лен­но­сти на­се­ле­ния Китая? В от­ве­те на­пи­ши­те чис­лен­ность на­се­ле­ния этого го­су­дар­ства в млн чел.

6. Решите си­сте­му уравнений  

В ответе запишите сумму решений системы.

7. Мас­штаб карты 1:100 000. Чему равно рас­сто­я­ние между го­ро­да­ми A и B (в км), если на карте оно со­став­ля­ет 2 см?

8.

На диа­грам­ме по­ка­за­но со­дер­жа­ние пи­та­тель­ных ве­ществ в сли­воч­ных су­ха­рях. Опре­де­ли­те по диа­грам­ме, в каких пре­де­лах на­хо­дит­ся со­дер­жа­ние уг­ле­во­дов.

*-к про­че­му от­но­сят­ся вода, ви­та­ми­ны и ми­не­раль­ные ве­ще­ства.

1) 45-55%

2) 55-65%

3) 65-75%

4) 75-80%

9. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют два­жды. Най­ди­те ве­ро­ят­ность того, что орел вы­па­дет ровно 1 раз.

10. Установите соответствие между функциями и их графиками.

ФУНКЦИИ 

А) 

Б) 

В) 

ГРАФИКИ

В таблице под каждой буквой укажите соответствующий номер.

11. Геометрическая про­грес­сия    за­да­на фор­му­лой   - го члена  . Ука­жи­те чет­вер­тый член этой прогрессии.

12. Найдите зна­че­ние вы­ра­же­ния  при 

13. Длину окружности   можно вы­чис­лить по фор­му­ле , где  — ра­ди­ус окружности (в метрах). Поль­зу­ясь этой формулой, най­ди­те радиус окружности, если её длина равна 78 м. (Считать ).

14. Решите неравенство: 

В ответе укажите номер правильного варианта.

1) 

2) 

3) 

4) 

15. Какое наи­боль­шее число ко­ро­бок в форме пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да раз­ме­ром 30×50×90 (см) можно по­ме­стить в кузов ма­ши­ны раз­ме­ром 2,4×3×2,7 (м)?

16.

В тре­уголь­ни­ке ABC BM — ме­ди­а­на и BH – высота. Известно, что AC = 216, HC = 54 и ∠ACB = 40°. Най­ди­те угол AMB. Ответ дайте в градусах.

17.

В угол ве­ли­чи­ной 70° впи­са­на окружность, ко­то­рая ка­са­ет­ся его сто­рон в точ­ках A и B. На одной из дуг этой окруж­но­сти вы­бра­ли точку C так, как по­ка­за­но на рисунке. Най­ди­те ве­ли­чи­ну угла ACB.

18. В пря­мо­уголь­ни­ке диагональ равна 10, а угол между ней и одной из сто­рон равен 30°. Най­ди­те площадь прямоугольника, делённую на .

19.

Найдите угол . Ответ дайте в градусах.

20. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Тре­уголь­ни­ка со сто­ро­на­ми 1, 2, 4 не существует.

2) Сумма углов лю­бо­го тре­уголь­ни­ка равна 360 градусам.

3) Се­ре­дин­ные пер­пен­ди­ку­ля­ры к сто­ро­нам тре­уголь­ни­ка пе­ре­се­ка­ют­ся в цен­тре его опи­сан­ной окружности.

Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.

21. Найдите зна­че­ние вы­ра­же­ния  если 

22. Первую по­ло­ви­ну трас­сы ав­то­мо­биль про­ехал со ско­ро­стью 55 км/ч, а вто­рую — со ско­ро­стью 70 км/ч. Най­ди­те сред­нюю ско­рость ав­то­мо­би­ля на про­тя­же­нии всего пути.

23. Найдите наи­мень­шее зна­че­ние вы­ра­же­ния и зна­че­ния x и y, при ко­то­рых оно до­сти­га­ет­ся  

24. Най­ди­те пло­щадь тра­пе­ции, диа­го­на­ли ко­то­рой равны 16 и 12, а сред­няя линия равна 10.

25. В тре­уголь­ни­ке ABC с тупым углом ABC про­ве­де­ны высоты AA₁ и CC₁. Докажите, что тре­уголь­ни­ки A₁BC₁ и ABC подобны.

26. В тре­уголь­ни­ке ABC бис­сек­три­са BE и ме­ди­а­на AD пер­пен­ди­ку­ляр­ны и имеют оди­на­ко­вую длину, рав­ную 96. Най­ди­те сто­ро­ны тре­уголь­ни­ка ABC .

Тренировочный вариант №2

1. Запишите в от­ве­те но­ме­ра выражений, зна­че­ния ко­то­рых положительны.

Номера за­пи­ши­те в по­ряд­ке воз­рас­та­ния без пробелов, за­пя­тых и дру­гих до­пол­ни­тель­ных символов.

2. В таб­ли­це при­ве­де­ны нор­ма­ти­вы по бегу на 30 мет­ров для уча­щих­ся 9-х классов.

Какую от­мет­ку по­лу­чит девочка, про­бе­жав­шая эту ди­стан­цию за 5,36 секунды?

3. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и b.

В ответе укажите номер правильного варианта.

Какое из при­ве­ден­ных утвер­жде­ний не­вер­но?

1) 

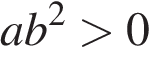
2) 

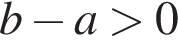
3) 

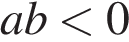
4) 

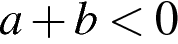
4. Чему равно зна­че­ние вы­ра­же­ния 

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1) 6

2) 12

3) 18

4) 36

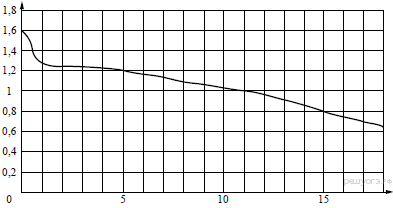
5. На ри­сун­ке по­ка­зан гра­фик раз­ря­да ба­та­рей­ки в кар­ман­ном фонарике. На го­ри­зон­таль­ной оси от­ме­ча­ет­ся время ра­бо­ты фо­на­ри­ка в часах, на вер­ти­каль­ной оси — на­пря­же­ние в вольтах. Опре­де­ли­те по рисунку, какое на­пря­же­ние будет да­вать ба­та­рей­ка через 5 часов ра­бо­ты фонарика. Ответ дайте в вольтах.

6. Решите урав­не­ние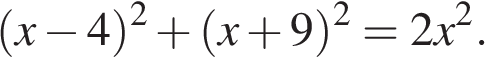 

7. Из объ­яв­ле­ния фирмы, про­во­дя­щей обу­ча­ю­щие се­ми­на­ры:

«Сто­и­мость уча­стия в се­ми­на­ре — 3000 р. с че­ло­ве­ка. Груп­пам от ор­га­ни­за­ций предо­став­ля­ют­ся скид­ки: от 3 до 10 че­ло­век — 5%; более 10 че­ло­век — 8%».

Сколь­ко руб­лей долж­на за­пла­тить ор­га­ни­за­ция, на­пра­вив­шая на се­ми­нар груп­пу из 4 че­ло­век?

8. На диа­грам­ме по­ка­за­но со­дер­жа­ние пи­та­тель­ных ве­ществ в четырёх видах продуктов. Опре­де­ли­те по диаграмме, в каких про­дук­тах со­дер­жа­ние уг­ле­во­дов пре­вы­ша­ет 50%.

В от­ве­те за­пи­ши­те но­ме­ра нуж­ных про­дук­тов без пробелов, за­пя­тых и дру­гих знаков.

*К дру­го­му от­но­сят­ся вода, ви­та­ми­ны и ми­не­раль­ные вещества.

1) какао

2) шоколад

3) сырки

4) сгущённое молоко

9. В сред­нем из каж­дых 80 по­сту­пив­ших в про­да­жу ак­ку­му­ля­то­ров 76 ак­ку­му­ля­то­ров заряжены. Най­ди­те ве­ро­ят­ность того, что куп­лен­ный ак­ку­му­ля­тор не заряжен.

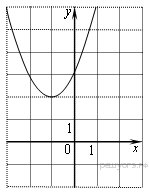
10. Найдите зна­че­ние 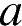 по гра­фи­ку функции 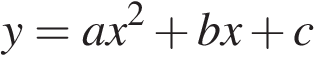, изоб­ра­жен­но­му на рисунке.

11. Арифметическая про­грес­сия за­да­на условиями: 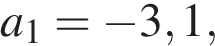 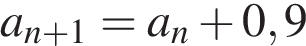. Най­ди­те сумму пер­вых 19 её членов.

12. Найдите значение выражения 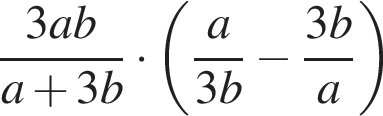 при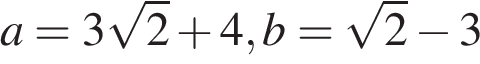 

13. Зная длину сво­е­го шага, че­ло­век может приближённо под­счи­тать пройденное им рас­сто­я­ние s по фор­му­ле s = nl, где n — число шагов, l — длина шага. Какое рас­сто­я­ние прошёл человек, если l = 50 см, n = 1100? Ответ вы­ра­зи­те в километрах.

14. На каком рисунке изображено множество решений неравенства ?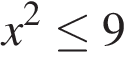

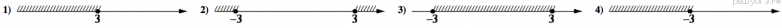
15.

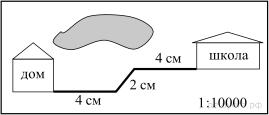 На карте по­ка­зан путь Лены от дома до школы. Лена из­ме­ри­ла длину каж­до­го участка и под­пи­са­ла его. Ис­поль­зуя рисунок, определите, длину пути (в м), если мас­штаб 1 см: 10000 см.

16.

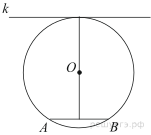
Радиус окруж­но­сти с цен­тром в точке O равен 85, длина хорды ABравна 80 (см. рисунок). Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k.

17.

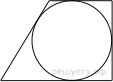
Радиус окружности, вписанной в трапецию, равен 16. Найдите высоту этой трапеции.

18. Периметр рав­но­бед­рен­но­го треугольника равен 16, а бо­ко­вая сторона — 5. Най­ди­те площадь треугольника.

19.

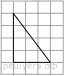
На ри­сун­ке изображён пря­мо­уголь­ный треугольник. Най­ди­те длину ме­ди­а­ны треугольника, проведённой из вер­ши­ны пря­мо­го угла.

20. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Тре­уголь­ни­ка со сто­ро­на­ми 1, 2, 4 не существует.

2) Смеж­ные углы равны.

3) Все диа­мет­ры окруж­но­сти равны между собой.

Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.

21. Решите урав­не­ние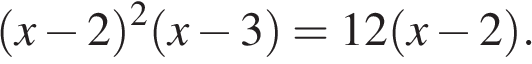 

22. Из пяти сле­ду­ю­щих утверждений о ре­зуль­та­тах матча хок­кей­ных команд "Транспортир" и "Линейка" че­ты­ре истинны, а одно — ложно. Определите, с каким сче­том закончился матч, и ука­жи­те победителя (если матч за­вер­шил­ся победой одной из команд). Ответ обоснуйте.

1) Вы­иг­рал "Транспортир".

2) Всего в матче было за­бро­ше­но менее 10 шайб.

3) Матч за­кон­чил­ся вничью.

4) Всего в матче было за­бро­ше­но более 8 шайб.

5) "Линейка" за­бро­си­ла более 3 шайб.

23. По­строй­те гра­фик функ­ции 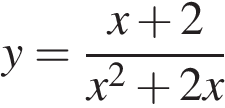 и определите, при каких зна­че­ни­ях  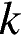пря­мая 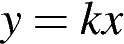имеет с гра­фи­ком одну общую точку.

24.

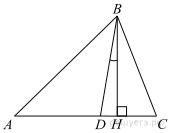
В тре­уголь­ни­ке АВС углы А и С равны 40° и 60° со­от­вет­ствен­но. Най­ди­те угол между вы­со­той ВН и бис­сек­три­сой BD.

25. В па­рал­ле­ло­грам­ме ABCD точка E — се­ре­ди­на сто­ро­ны AB. Известно, что EC=ED. Докажите, что дан­ный па­рал­ле­ло­грамм — прямоугольник.

26. В пря­мо­уголь­ном тре­уголь­ни­ке ABC с пря­мым углом B, про­ве­де­на бис­сек­три­са угла A. Известно, что она пе­ре­се­ка­ет се­ре­дин­ный пер­пен­ди­ку­ляр, проведённый к сто­ро­не BC в точке K. Най­ди­те угол BCK, если известно, что угол ACB равен 40°.

Тематическое планирование курса.

Входная диагностическая работа

Вариант 1

1. Най­ди­те зна­че­ние вы­ра­же­ния  

Ответ_________________

2.

Завуч школы под­вел итоги по вы­бо­ру предметов для сдачи ЕГЭ уча­щи­ми­ся 11-х классов. Ре­зуль­та­ты представлены на диаграмме. Сколь­ко примерно уча­щих­ся выбрали для сдачи ЕГЭ физику?

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1) 16

2) 12

3) 14

4) 8

Ответ_____________

3. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и b.

В ответе укажите номер правильного варианта.

Какое из сле­ду­ю­щих утвер­жде­ний от­но­си­тель­но этих чисел яв­ля­ет­ся верным?

1) a³​0

2) a − b  0

3) ab 

4) a + b  1

Ответ_____________

4. Найдите зна­че­ние вы­ра­же­ния 

1) 120

2) 

3) 

4) 

Ответ_____________

5. На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику, через сколько минут с момента запуска двигатель нагреется до 40°С.

Ответ ____________

6. Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

Ответ _______________

7. Для при­го­тов­ле­ния фарша взяли го­вя­ди­ну и сви­ни­ну в от­но­ше­нии 9:1. Какой про­цент в фарше со­став­ля­ет свинина?

Ответ ______________

8. 

На диа­грам­ме пред­став­ле­но рас­пре­де­ле­ние ко­ли­че­ства поль­зо­ва­те­лей не­ко­то­рой со­ци­аль­ной сети по стра­нам мира. Всего в этой со­ци­аль­ной сети 12 млн поль­зо­ва­те­лей.

Какое из сле­ду­ю­щих утвер­жде­ний не­вер­но?

1) Поль­зо­ва­те­лей из Укра­и­ны боль­ше, чем поль­зо­ва­те­лей из Ка­зах­ста­на.

2) Поль­зо­ва­те­лей из Рос­сии вдвое боль­ше, чем поль­зо­ва­те­лей из Укра­и­ны.

3) При­мер­но треть поль­зо­ва­те­лей — не из Рос­сии.

4) Поль­зо­ва­те­лей из Укра­и­ны и Бе­ла­ру­си более 3 млн че­ло­век.

Ответ ____________

9. На та­рел­ке лежат оди­на­ко­вые на вид пи­рож­ки: 4 с мясом, 8 с ка­пу­стой и 3 с виш­ней. Петя на­у­гад вы­би­ра­ет один пи­ро­жок. Най­ди­те ве­ро­ят­ность того, что он ока­жет­ся с виш­ней.

Ответ ____________

10.

На ри­сун­ке изоб­ражён гра­фик квад­ра­тич­ной функ­ции y = f(x).

Какие из сле­ду­ю­щих утвер­жде­ний о дан­ной функ­ции не­вер­ны? За­пи­ши­те их но­ме­ра.­

1) f(x) x 

2) Наи­боль­шее зна­че­ние функ­ции равно 3

3) f(0)  f(4)

Если от­ве­тов не­сколь­ко, за­пи­ши­те их в по­ряд­ке воз­рас­та­ния

Ответ ____________

11. Упростите вы­ра­же­ние , най­ди­те его зна­че­ние при . В ответ за­пи­ши­те полученное число.

Ответ ____________

12.

Картинка имеет форму прямоугольника со сторонами 14 см и 27 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 558 см. Какова ширина окантовки? Ответ дайте в сантиметрах.

Ответ ____________

13.

В остроугольном треугольнике ABC высота AH равна  а сторона ABравна 50. Найдите cosB.

Ответ ____________

14.

 К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO. Най­ди­те ра­ди­ус окружности, если AB = 14 см, AO = 50 см.

Ответ ____________

15. Периметр квад­ра­та равен 56. Най­ди­те площадь квадрата.

Ответ ____________

16. На клетчатой бумаге с размером клетки 1х1 изображён ромб. Найдите длину его большей диагонали.

Ответ ____________

Входная диагностическая работа

Вариант 2

1. Найдите зна­че­ние выражения: 

Ответ ___________

2. В таб­ли­це даны ре­зуль­та­ты за­бе­га девочек 8-го клас­са на ди­стан­цию 60 м. Зачёт вы­став­ля­ет­ся, если по­ка­за­но время не хуже 10,8 с.

Укажите номера дорожек, по которым бежали девочки, получившие зачёт.

1) I,III

2) только IV

3) II, IV

4) только II

Ответ ___________

3. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a, b и с.

Из сле­ду­ю­щих утвер­жде­ний вы­бе­ри­те вер­ное.

В ответе укажите номер правильного варианта.

1) a − c  0

2) c − a 

3) a − b 

4) b − c  0

Ответ ___________

4. Вычислите: 

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1) 

2) 

3) 

4) 

Ответ ___________

5. При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,2 В до 0,8 В.

Ответ ___________

6. Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

Ответ ___________

7. На пост пред­се­да­те­ля школьного со­ве­та претендовали два кандидата. В го­ло­со­ва­нии приняли уча­стие 120 человек. Го­ло­са между кан­ди­да­та­ми распределились в от­но­ше­нии 3:5. Сколь­ко голосов по­лу­чил победитель?

Ответ ___________

8. На диа­грам­ме пред­став­ле­ны не­ко­то­рые из круп­ней­ших по чис­лен­но­сти на­се­ле­ния стран мира.

Чис­лен­ность на­се­ле­ния ка­ко­го го­су­дар­ства при­мер­но в 6 раз мень­ше чис­лен­но­сти на­се­ле­ния Индии?

В от­ве­те напишите чис­лен­ность населения этой стра­ны в млн чел.

Ответ ___________

9. На та­рел­ке лежат оди­на­ко­вые на вид пи­рож­ки: 4 с мясом, 5 с рисом и 21 с повидлом. Андрей на­у­гад вы­би­ра­ет один пи­ро­жок. Най­ди­те ве­ро­ят­ность того, что он ока­жет­ся с повидлом.

Ответ ___________

10.

На ри­сун­ке изоб­ражён гра­фик квад­ра­тич­ной функ­ции y = f(x).

Какие из сле­ду­ю­щих утвер­жде­ний о дан­ной функ­ции не­вер­ны? За­пи­ши­те их но­ме­ра в по­ряд­ке возрастания.

1) Функ­ция воз­рас­та­ет на про­ме­жут­ке (−∞;  −1].

2) Наи­боль­шее зна­че­ние функ­ции равно 8.

3) f(−4) ≠ f(2).

Ответ ___________

11. Найдите зна­че­ние выражения    при  

Ответ ___________

12.

Картинка имеет форму прямоугольника со сторонами 14 см и 27 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 558 см. Какова ширина окантовки? Ответ дайте в сантиметрах.

Ответ ___________

13.

В тре­уголь­ни­ке ABC BM — ме­ди­а­на и BH — высота. Известно, что AC = 104, HC = 26 и ∠ACB = 75°. Най­ди­те угол AMB. Ответ дайте в градусах.

Ответ ___________

14.

Прямая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окружности. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 60°. Най­ди­те ве­ли­чи­ну угла OMK. Ответ дайте в градусах.

Ответ ___________

15. Периметр квад­ра­та равен 40. Най­ди­те площадь квадрата.

Ответ ___________

16. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь. Ответ ___________