2. Изучение нового учебного материала (способов действий). Цели для преподавателя: - обеспечить понимание планируемого результата деятельности, основных путей его достижения; -способствовать развитию познавательных способностей обучающихся, посредством организации самостоятельной работы. Цели для обучающихся: - познакомиться с сервисом сетевого уровня - рассмотреть подходы к организации сетевого уровня - познакомиться с подходом с установлением соединения - познакомиться с подходом с без соединений Цели этапа занятия достигаются посредством: - обеспечения понимания планируемого результата деятельности, основных путей его достижения; - определения критериев, позволяющих обучающимся самостоятельно определять степень достижения запланированного результата; - организации активной самостоятельной деятельности обучающихся по написанию лекции во время занятия.
| 2. Теоретическая часть. Основной задачей сетевого уровня является маршрутизация пакетов. Пакеты маршрутизируются всегда, независимо от того, какую внутреннюю организацию имеет транспортная среда - с виртуальными каналами или дейтаграммную. Разница лишь в том, что в первом случае этот маршрут устанавливается один раз для всех пакетов, а во втором - для каждого пакета. В первом случае говорят иногда о маршрутизации сессии, потому что маршрут устанавливается на все время передачи данных пользователя, т.е. сессии.
Алгоритм маршрутизации - часть программного обеспечения сетевого уровня. Он отвечает за определение, по какой линии отправлять пакет дальше. Вне зависимости от того, выбирается маршрут для сессии или для каждого пакета в отдельности, алгоритм маршрутизации должен обладать рядом свойств: корректностью, простотой, устойчивостью, стабильностью, справедливостью и оптимальностью. Если корректность и простота комментариев не требуют, то остальные свойства надо разъяснить.
Алгоритм маршрутизации должен быть устойчивым, т.е. сохранять работоспособность независимо ни от каких сбоев или отказов в сети, изменений в ее топологии (отключение хостов, машин транспортной подсети, разрушения каналов и т.п). Алгоритм маршрутизации должен адаптироваться ко всем таким изменениям, не требуя перезагрузки сети или остановки абонентских машин.
Стабильность алгоритма - также весьма важный фактор. Существуют алгоритмы маршрутизации, которые никогда не сходятся к какому-либо равновесному состоянию, как бы долго они ни работали. Это означает, что адаптация алгоритма к изменениям в конфигурации транспортной среды может оказаться весьма продолжительной. Более того, она может оказаться сколь угодно долгой.
Справедливость значит, что все пакеты, вне зависимости от того, из какого канала они поступили, будут обслуживаться равномерно, никакому направлению не будет отдаваться предпочтение, для всех абонентов будет всегда выбираться оптимальный маршрут. Надо отметить, что справедливость и оптимальность часто могут вступать в противоречие друг с другом.
Прежде чем искать компромисс между оптимальностью и справедливостью, мы должны решить, что является критерием оптимизации. Один из возможных критериев - минимизация средней задержки пакета. Другой - максимизация пропускной способности сети. Однако эти критерии конфликтуют. Согласно теории массового обслуживания, если система с очередями функционирует близко к своему насыщению, то задержка в очереди увеличивается. Как компромисс, во многих сетях минимизируется число переходов между маршрутизаторами - один такой переход мы будем называть скачком (hop). Уменьшение числа скачков сокращает маршрут, а следовательно, сокращает задержку, а также минимизирует потребляемую пропускную способность при передаче пакета.
Алгоритмы маршрутизации можно разбить на два больших класса: адаптивные и неадаптивные. Неадаптивные алгоритмы не принимают в расчет текущую загрузку сети и состояние топологии. Все возможные маршруты вычисляются заранее и загружаются в маршрутизаторы при загрузке сети. Такая маршрутизация называется статической маршрутизацией.
Адаптивные алгоритмы, наоборот, определяют маршрут, исходя из текущей загрузки сети и топологии. Адаптивные алгоритмы различаются тем, где и как они получают информацию (локально от соседних маршрутизаторов или глобально от всех), когда они меняют маршрут (каждые Т секунд, когда меняется нагрузка, когда меняется топология), какая метрика используется при оптимизации (расстояние, число скачков, ожидаемое время передачи).
Прежде чем мы приступим к рассмотрению конкретных алгоритмов маршрутизации, сформулируем принцип оптимальности. Этот принцип утверждает, что если маршрутизатор J находится на оптимальном пути между маршрутизаторами I и K, то оптимальный маршрут между J и K принадлежит этому оптимальному пути. Это так, поскольку существование между J и K оптимального маршрута, отличного от части маршрута между I и K, противоречил бы утверждению об оптимальности маршрута между I и K. Дело в том, что если рассмотреть маршрут от I до К, как от I до J (назовем его S1) и от J до К (назовем его S2), то если между J и К есть маршрут лучше, чем S2, например S3, то маршрут S1S2 не может быть лучшим. Взяв конкатенацию маршрутов S1S3, мы получим лучший маршрут, чем маршрут S1S2.
Следствием из принципа оптимальности является утверждение, что все маршруты к заданной точке сети образуют дерево с корнем в этой точке.
Поскольку дерево захода - это дерево, то там нет циклов, поэтому каждый пакет будет доставлен за конечное число шагов. На практике все может оказаться сложнее. Маршрутизаторы могут выходить из строя, и, наоборот, появляться новые, каналы могут выходить из строя, разные маршрутизаторы могут узнавать об этих изменениях в разное время и т.д. и т.п. Маршрутизация по наикратчайшему пути. Наше изучение алгоритмов маршрутизации мы начнем со статического алгоритма, широко используемого на практике в силу его простоты. Идея этого алгоритма состоит в построении графа транспортной среды, где вершины - маршрутизаторы, а дуги - линии связи. Алгоритм находит для любой пары маршрутизаторов, а точнее абонентов, подключенных к этим маршрутизаторам, наикратчайший маршрут в этом графе.
Проиллюстрируем идею алгоритма нахождения наикратчайшего пути на рисунке 5-6 (стрелками обозначены задействованные узлы). На дугах этого графа указаны веса, которые представляют расстояние между дугами. Расстояние можно измерять в переходах, а можно в километрах. Возможны и другие меры. Например, дуги графа могут быть размечены весами, величина которых равна средней задержке пакетов в соответствующем канале. В графе с такой разметкой наикратчайший путь - наибыстрейший путь, хотя он не обязательно имеет минимальное число переходов или километров.
В общем случае веса на дугах могут быть функциями от расстояния, пропускной способности канала, среднего трафика, стоимости передачи, средней длины очереди в буфере маршрутизатора к данному каналу и других факторов. Изменяя весовую функцию, алгоритм будет вычислять наикратчайший путь в смысле заданной метрики.
Известно несколько алгоритмов вычисления наикратчайшего пути в графе. Один из них предложил голландский математик Эдсгер Дейкстра. Идею этого алгоритма можно описать так. Все вершины в графе, смежные исходной вершине, помечают расстоянием (оно указано в скобках) до исходной вершины. Изначально никаких путей не известно и все вершины помечены бесконечностью. По мере работы алгоритма и нахождения путей, метки могут меняться. Метки могут быть двух видов: либо пробными, либо постоянными. Изначально все метки пробные. Когда обнаруживается, что метка представляет наикратчайший путь до исходной вершины, она превращается в постоянную метку и никогда более не меняется.
На рисунке 5-6 показан процесс построения маршрута из А в D. Помечаем вершину А как постоянную (вершина, закрашенная черным цветом). Все вершины, смежные А, помечаем как временные (эти вершины не закрашены), а также указываем в метке их вершину, из которой мы апробировали данную вершину. Это позволит нам впоследствии изменить маршрут, если надо. Кроме этого, все вершины, смежные А, помечаем расстоянием от А до этой вершины. Из всех смежных вершин мы выберем ту, расстояние до которой самое короткое, и ее объявляем рабочей. Таким образом, мы выберем на первом шаге вершину В, а затем Е.
Самое интересное возникнет на шаге (d). В соответствии с принципом наикратчайшего пути мы в качестве рабочей выберем вершину G. Теперь, на шаге (е), когда мы начнем искать вершины, смежные Н, то увидим, что путь F до Н короче, чем от G до Н. Поэтому на шаге (е) мы в качестве рабочей возьмем вершину F, а затем Н. На рисунке 5-7 дано описание алгоритма Дейкстры. Надо сделать оговорку, что этот алгоритм строит наикратчайший путь, начиная от точки доставки, а не от точки отправления. Поскольку граф не ориентированный, то это никакого влияния на построение пути не оказывает. Маршрутизация лавиной. Другим примером статического алгоритма может служить следующий алгоритм: каждый поступающий пакет отправляют по всем имеющимся линиям, за исключением той, по которой он поступил. Ясно, что если ничем не ограничить число повторно генерируемых пакетов, то их число может расти неограниченно. Время жизни пакета ограничивают областью его распространения. Для этого в заголовке каждого изначально генерируемого пакета устанавливается счетчик переходов. При каждой пересылке этот счетчик уменьшается на единицу. Когда он достигает нуля, пакет сбрасывается и далее не посылается. В качестве начального значения счетчика выбирают наихудший случай, например, диаметр транспортной подсети.
Другим приемом, ограничивающим рост числа дублируемых пакетов, является отслеживание на каждом маршрутизаторе тех пакетов, которые через него однажды уже проходили. Такие пакеты сбрасываются и больше не пересылаются. Для этого каждый маршрутизатор, получая пакет непосредственно от абонентской машины, помечает его надлежащим числом. В свою очередь, каждый маршрутизатор ведет список номеров, сгенерированных другим маршрутизатором. Если поступивший пакет уже есть в списке, то этот пакет сбрасывается. Для предотвращения безграничного роста списка вводят ограничительную константу k. Считается, что все номера, начиная с k и далее, уже встречались.
Несмотря на кажущуюся неуклюжесть, этот алгоритм применяется, например, в распределенных базах данных, когда надо параллельно обновить данные во всех базах одновременно. Этот алгоритм всегда находит наикратчайший маршрут за самое короткое время, поскольку все возможные пути просматриваются параллельно.
Маршрутизация на основе потока.
Рассмотрим статический алгоритм маршрутизации на основе потока, который учитывает как топологию, так и загрузку транспортной подсети.
В некоторых сетях трафик между каждой парой узлов известен заранее и относительно стабилен. Например, в случае взаимодействия сети торгующих организаций со складом. Время подачи отчетов, размер и форма отчетов известны заранее. В этих условиях, зная пропускную способность каналов, можно с помощью теории массового обслуживания вычислить среднюю задержку пакета в канале. Тогда нетрудно построить алгоритм, вычисляющий путь с минимальной задержкой пакета между двумя узлами.
Для реализации этой идеи нам нужно о каждой транспортной среде заранее знать следующее:
Все современные транспортные подсети используют динамическую маршрутизацию, а не статическую. Один из наиболее популярных алгоритмов - маршрутизация по вектору расстояния. Этот алгоритм построен на идеях алгоритмов нахождения кратчайшего пути Беллмана-Форда и алгоритма Форда-Фолкерсона, определяющего максимальный поток в графе. Он изначально использовался в сети ARPA и используется по сей день в протоколе RIP (Routing IP).
Алгоритм маршрутизации по вектору расстояния устроен следующим образом: у каждого маршрутизатора в транспортной подсети есть таблица расстояний до каждого маршрутизатора, принадлежащего подсети. Периодически маршрутизатор обменивается такой информацией со своими соседями и обновляет информацию в своей таблице. Каждый элемент таблицы состоит из двух полей: первое - номер канала, по которому надо отправлять пакеты, чтобы достичь нужного места, второе - величина задержки до места назначения. Величина задержки может быть измерена в разных единицах: числе переходов, миллисекундах, длине очереди на канале и т.д. Фактически в протоколе использовалась версия алгоритма, где эту задержку определяли не на основе пропускной способности канала, а на основе длины очереди к каналу.
Каждые Т секунд маршрутизатор шлет своим соседям свой вектор задержек до всех маршрутизаторов в подсети. В свою очередь, он получает такие же вектора от своих соседей. Кроме этого, он постоянно замеряет задержки до своих соседей. Поэтому, имея вектора расстояний от соседей и зная расстояние до них, маршрутизатор всегда может вычислить кратчайший маршрут до определенного места в транспортной среде.
Алгоритм маршрутизации по вектору расстояния теоретически работает хорошо, но у него есть один недостаток: он очень медленно реагирует на разрушения каналов в транспортной среде. Информация о появлении хорошего маршрута в подсети распространяется более или менее быстро, а вот данные о потере, разрушении какого-то маршрута распространяются не столь быстро.
Одним из решений этой проблемы является следующий прием. Алгоритм работает так, как было описано, но при передаче вектора по линии, по которой направляются пакеты для маршрутизатора Х, т.е. по которой достижим маршрутизатор Х, расстояние до Х указывается как бесконечность.
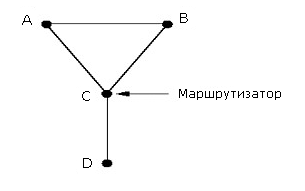
Однако и в алгоритме разделения направлений есть «дыры». Рассмотрим подсеть на рисунке 5-12. Если линия между С и D будет разрушена, то С сообщит об этом А и В. Однако А знает, что у В есть маршрут до D, а В знает, что такой маршрут есть и у А. И опять мы «сваливаемся» в проблему бесконечного счетчика.
Рисунок 5-12. Случай, при котором разделение направлений не помогает
Маршрутизация по состоянию канала.
 Алгоритм маршрутизации по вектору расстояний использовался в сети ARPANET до 1979 года, после чего он был заменен. Тому было две основных причины. Первая - пропускная способность канала никак не учитывалась, поскольку основной мерой задержки была длина очереди. Вторая проблема – медленная сходимость алгоритма при изменениях. По этим причинам был создан новый алгоритм маршрутизации по состоянию канала.
Основная идея построения этого алгоритма проста и состоит из пяти основных шагов:
Определить своих соседей и их сетевые адреса.
Измерить задержку или оценить затраты на передачу до каждого соседа.
Сформировать пакет, где указаны все данные, полученные на шаге 2.
Послать этот пакет всем другим маршрутизаторам.
Вычислить наикратчайший маршрут до каждого маршрутизатора.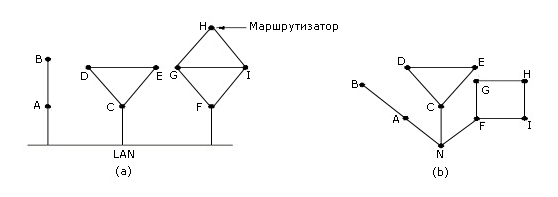
 Топология и все задержки оцениваются экспериментально и сообщаются всем узлам. После этого можно использовать, например, алгоритм Дейкстры для вычисления наикратчайшего маршрута. Теперь рассмотрим подробнее эти пять шагов.
При загрузке маршрутизатор прежде всего определяет, кто его соседи. Для этого он рассылает по всем своим линиям точка-точка специальный пакет HELLO. В ответ все маршрутизаторы отвечают, указывая свое уникальное имя. Имя маршрутизатора должно быть уникальным в сети, чтобы избежать неоднозначностей. Если же два и более маршрутизатора соединены одним каналом, как на рисунке 5-13 (а), то этот канал в графе связей представляют отдельным, искусственным узлом (рисунок 5-13 (b)).
Рисунок 5-13. Определение соседей
Оценка затрат до каждого соседа происходит с помощью другого специального пакета EСHO. Это пакет рассылается всем соседям, при этом замеряется задержка от момента отправки этого пакета до момента его возвращения. Все, кто получает такой пакет, обязаны отвечать незамедлительно. Такие замеры делают несколько раз и вычисляют среднее значение. Таким образом, длина очереди к каналу не учитывается.
Здесь есть одна тонкость: учитывать загрузку в канале или нет? Если учитывать, то задержку надо замерять от момента поступления пакета в очередь к каналу. Если не учитывать, то от момента, когда пакет достиг головы очереди. Есть доводы, как в пользу учета нагрузки, так и против такого учета. Учитывая нагрузку, мы можем выбирать между двумя и более каналами с одинаковой пропускной способностью, получая лучшую производительность. Однако можно привести примеры, когда ее учет вызывает проблемы.
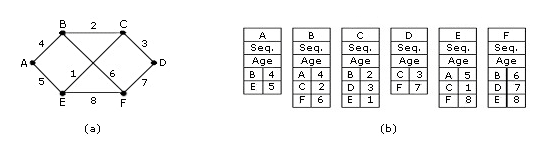
После того как измерения выполнены, можно сформировать пакет о состоянии каналов. На рисунке 5-14 показаны пакеты для примера сети. В пакете указаны: отправитель, последовательное число, возраст (назначение этих полей станет ясно позднее), список соседей и задержки до них. Формирование таких пакетов не вызывает проблем. Основной вопрос - когда их формировать? Периодически, с каким-то интервалом, или по особому событию, когда в транспортной подсети произошли какие-то существенные изменения?
Рисунок 5-14. Формирование пакетов состояния канала
Наиболее хитрая часть этого алгоритма – как надежно распространить пакеты о состоянии каналов (СК-пакеты)? Как только СК-пакет получен и включен в работу, маршрутизатор будет его использовать при определении маршрута. При неудачном распространении СК-пакетов разные маршрутизаторы могут получить разное представление о топологии транспортной среды, что может приводить к возникновению циклов, недостижимых машин и другим проблемам.
|
47
7
План-конспект урока по теме Сервисы сетевого уровня 