Векторы в пространстве

ТЕМА ЛЕКЦИИ:

«МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ»

ПЛАН ЛЕКЦИИ

• Определение матрицы, элементы матриц
• Виды матриц
• Линейные операции над матрицами

1. Определение матрицы, элементы матриц

Основные определения

МАТРИЦЕЙ называется множество чисел, образующих прямоугольную таблицу, состоящую из n строк и m столбцов.

Общий вид матрицы:

Числа а 11 , а 12 , …, а 1m , …, а n1 , а n2 , …,а nm называются элементами матриц.

2. Виды матриц

Матрица называется прямоугольной , если число строк матрицы не равно числу столбцов (n≠m).

Пример:

А=

Матрица порядка 2 х 3.

Матрица называется КВАДРАТНОЙ, если число строк равно числу столбцов (n=m).

Пример:

А =

Матрица второго порядка.

Диагональ, содержащую элементы а 11 , а 22 , …, а nn , называют главной.

Пример:

А=

Диагональ, содержащую элементы а 1n , а 2,n-1 , …, а n1 , называют побочной.

Пример:

Квадратная матрица называется диагональной , если у нее отличны от нуля только элементы, стоящие на главной диагонали.

Пример:

А=

Диагональная матрица 3-го порядка.

Диагональная матрица называется скалярной , если числа главной диагонали равны между собой.

Пример:

А=

Скалярная матрица 3-го порядка.

Скалярная матрица называется единичной , если все числа главной диагонали равны единице.

Пример:

Е=

Единичная матрица 3-го порядка.

Матрица называется НУЛЕВОЙ , если все ее элементы равны нулю.

Пример:

В=

Нулевая матрица 2-го порядка.

Если количество строк в прямоугольной матрице равно 1, то эта матрица называется матрицей-строкой.

С= (1 -2 4 6 -2)

Если количество столбцов в прямоугольной матрице равно 1, то эта матрица называется матрица - столбец.

Равенство матриц

Две матрицы называются равными , если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны.

3. Линейные операции над матрицами

• Суммой матриц А и В называется матрица элементы которой равны сумме соответствующих элементов матриц А и В.

Складывать можно матрицы, имеющие одинаковый порядок.

+ =

=.

Пример:

+ =

= =

2 . Произведением матрицы А на число k называется матрица каждый элемент которой равен k∙a ij .

=

Пример:

=

=

3. Умножение матриц

Рассмотрим умножение квадратных матриц второго порядка.

Пусть и В =

Тогда:

.

Пример:

=

= =

=

Нелинейные операции над матрицами

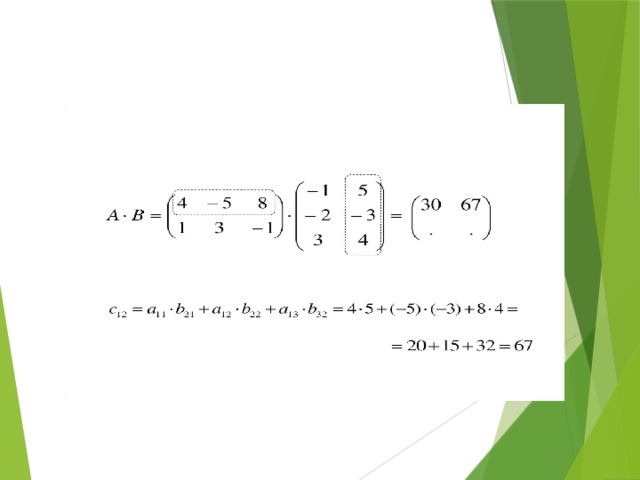
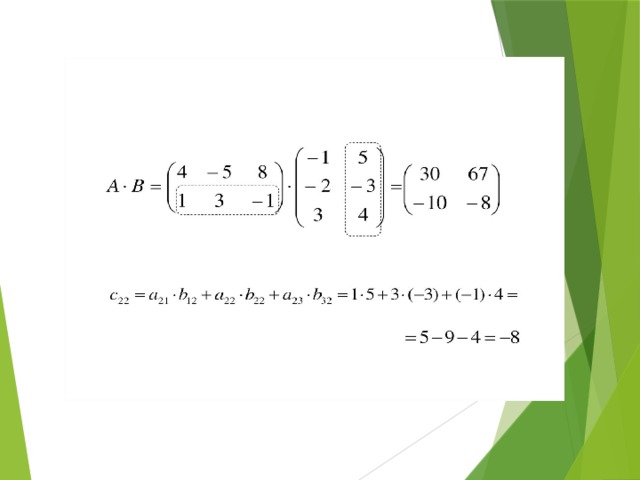
Вычислить АВ

Спасибо за внимание!!!

МОСКВА, 2009

ООО "РЕЗОЛЬВЕНТА"