Интерактивная лекция "Основы алгебры векторов"

• Основы алгебры векторов

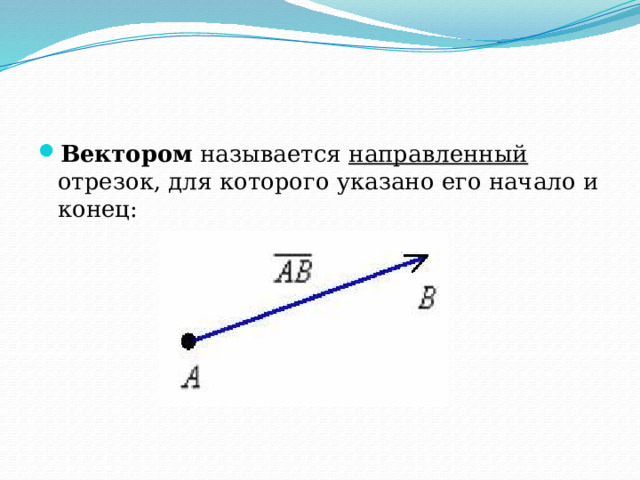
• Вектором называется направленный отрезок, для которого указано его начало и конец:

Уильям Гамильтон

• Гораздо раньше векторов в науку были введены кватернионы. Эти и в самом деле странные величины придумал Гамильтон.

Жозеф Луи Лагранж

• Создатели квантовой механики очень обязаны трудам Гамильтона и Лагранжа бывших не только физиками, но и превосходными математиками.

КВАТЕРНИОН

• Кватернион (выражаемый с помощью четверки чисел) и обычный вещественный вектор — совершенно разные понятия.
• В XIX в. его появление было преждевременным

Лорд Кельвин

• Кватернион исследовали известные английские ученые Тэйт и лорд Кельвин. Последнему принадлежит большая книга «Кватернионы».

Гиббс

• Несколько позже Гамильтона жил известный вам в другой связи американский ученый Гиббс.

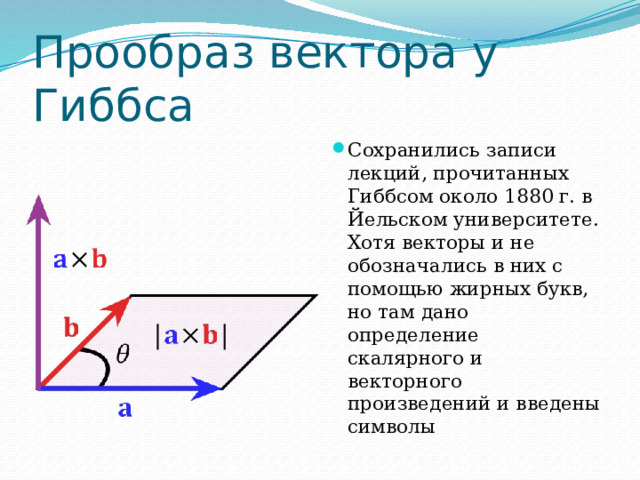
Прообраз вектора у Гиббса

• Сохранились записи лекций, прочитанных Гиббсом около 1880 г. в Йельском университете. Хотя векторы и не обозначались в них с помощью жирных букв, но там дано определение скалярного и векторного произведений и введены символы

Тейт

• Идеи Гиббса об использовании векторов не получили немедленного признания.
• Например, английский ученый Тейт утверждал, что пользоваться векторами неудобно

• Нам это удивительно, мы, напротив, не видим, зачем нужны кватернионы, которыми увлекался Тейт, где они могут найти применение?
• Правда, с появлением квантовой механики некоторые прежде непонятные величины приобретают важное значение.

• Гамильтон придумывает заумную вещь (кватернионы) и возвращается к своим обычным делам

• А спустя некоторое время после странного изобретения Гамильтона на сцене появились более естественные и удобные, чем кватернионы, величины — векторы.

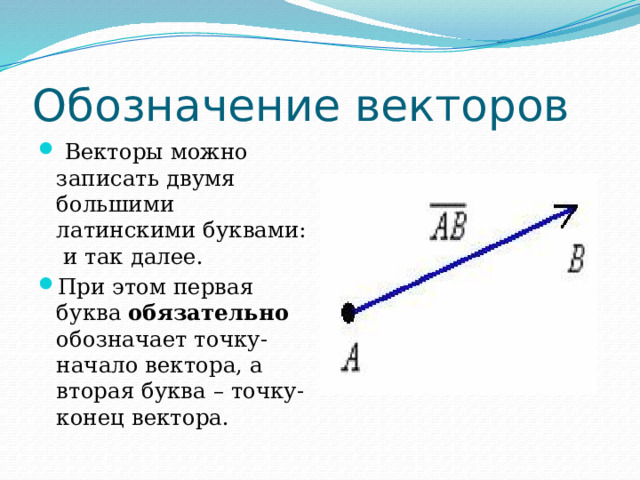
Обозначение векторов

• Векторы можно записать двумя большими латинскими буквами:  и так далее.
• При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.

Обозначение векторов

• Векторы также записывают маленькими латинскими буквами:  В частности, наш вектор  можно для краткости переобозначить маленькой латинской буквой .

Модуль вектора

• Длиной или модулем ненулевого вектора   называется длина отрезка АВ .

• Длина вектора обозначается знаком модуля

Нулевой вектор

• Нулевой вектор–это вектор, у которого вектора и начало совпадают.
• Обозначается

• Длина нулевого вектора  равна нулю

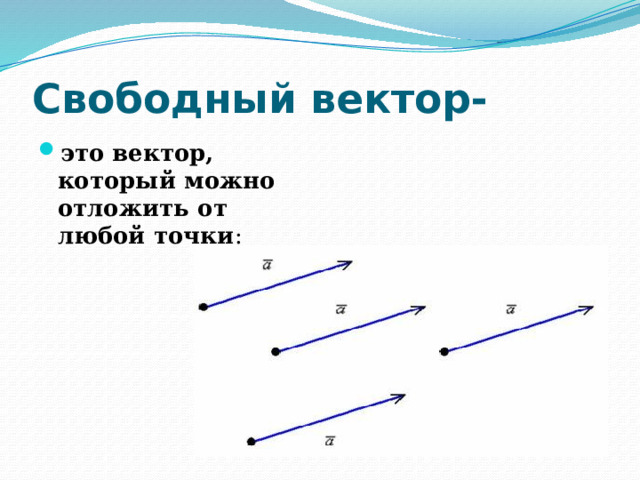
Свободный вектор-

• это вектор, который можно отложить от любой точки :

Действия с векторами

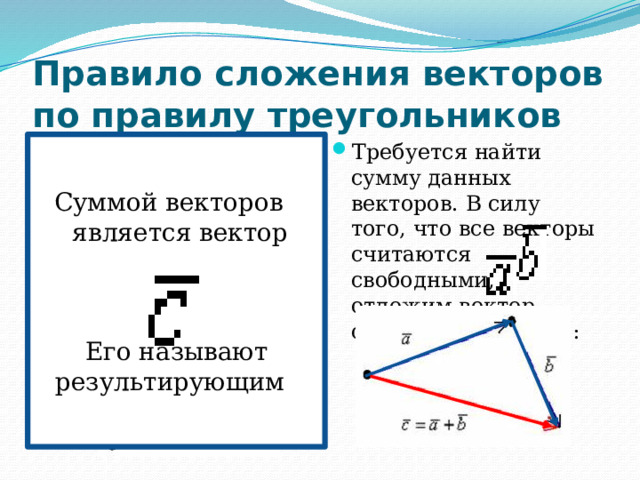
Правило сложения векторов по правилу треугольников

Суммой векторов    является вектор

Его называют результирующим .

• Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор   от конца вектора :

• Рассмотрим два произвольных ненулевых вектора

  и :

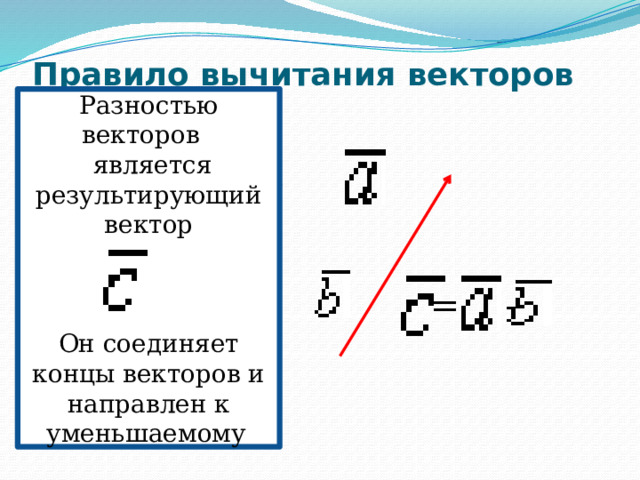
Правило вычитания векторов

Разностью векторов    является результирующий

вектор

Он соединяет концы векторов и направлен к уменьшаемому .

• Рассмотрим разность векторов -

= -

Коллинеарность векторов

• Два вектора называются коллинеарными ,
• если они лежат на одной прямой или на параллельных прямых

Коллинеарность векторов

• Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными .
• Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены

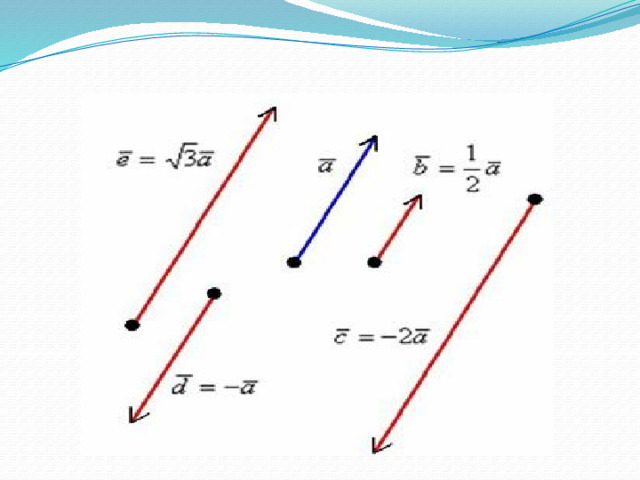
Произведение вектора на число

Векторы   и  сонаправлены при   и противоположно направлены при .

• Произведением ненулевого вектора  на

число   является такой

вектор , длина

которого равна ,

• Два вектора равны, если они сонаправлены и имеют одинаковую длину .

• Любые два вектора, сумма которых равна нулевому вектору, называются противоположными . Вектор, протилоположный вектору а , обозначается — а

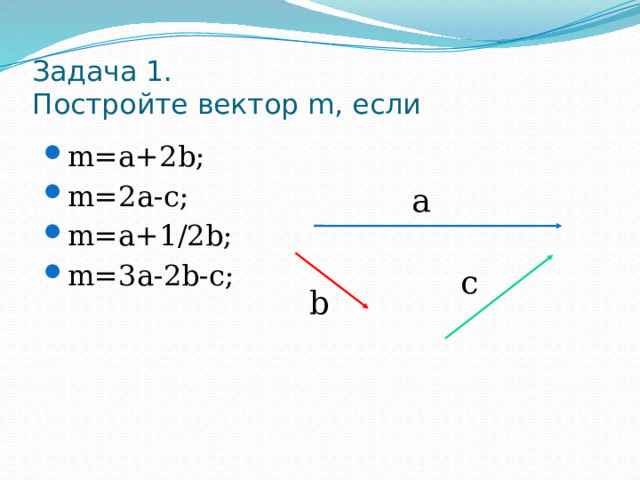
Задача 1. Постройте вектор m, если

• m=a+2b; m=2a-c; m=a+1/2b; m=3a-2b-c;
• m=a+2b;
• m=2a-c;
• m=a+1/2b;
• m=3a-2b-c;

а

c

b

КООРДИНАТЫ ВЕКТОРА НА ПЛОСКОСТИ

• Рассмотрим координатную плоскость и в ней единичные векторы  i и j , которые сонаправлены осям координат, и длина которых равна единичному отрезку: эти векторы называются базисными

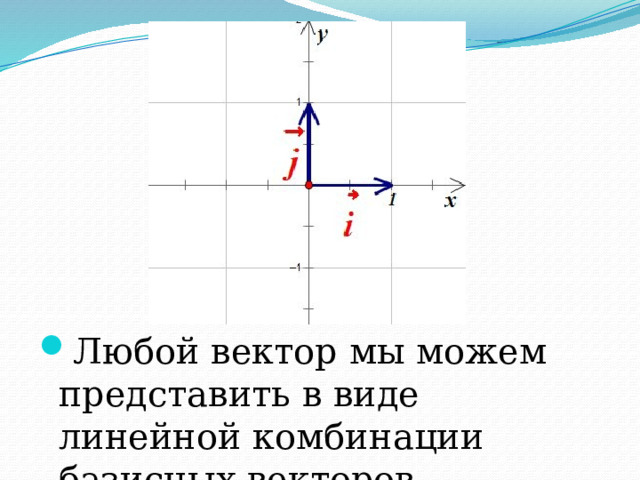
• Любой вектор мы можем представить в виде линейной комбинации базисных векторов

РАЗЛОЖЕНИЕ ВЕКТОРА ПО БАЗИСНЫМ

• а=2i+3j
• b=2i-3j
• c=-4i+3j

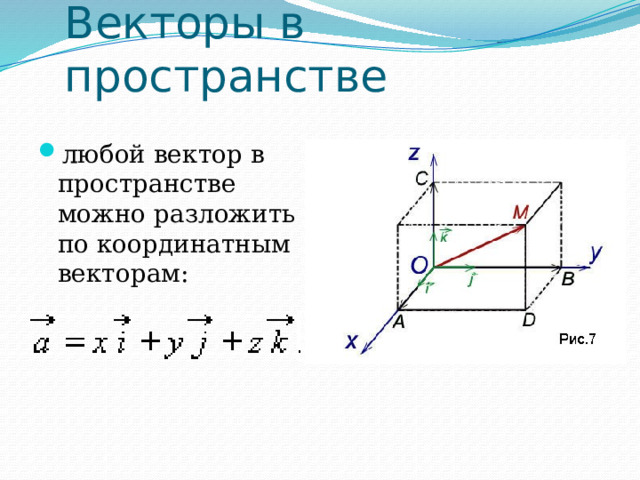
Векторы в пространстве

• любой вектор в пространстве можно разложить по координатным векторам:

Координаты вектора (на плоскости и в пространстве)

• Каждая координата вектора равна разности соответствующих координат его конца и начала .

Сумма и разность векторов

Умножение вектора на число

Модуль (длина) вектора

| а|=√а 1 2 +а 2 2 +а 3 2

Задача 2

• 1) Запишите векторы а и b, заданные координатами точек начала А(3;-1;5) и конца В(7;4;-2), и С (0; -1; 5) и D(8; -2; 1)соответственно. 2)Найдите координаты векторов е и n, если е=-2a+b, n=3b-a 3)Найдите модуль вектора е. 4)Найдите длину вектора n .
• 1) Запишите векторы а и b, заданные координатами точек начала А(3;-1;5) и конца В(7;4;-2), и С (0; -1; 5) и D(8; -2; 1)соответственно. 2)Найдите координаты векторов е и n, если е=-2a+b, n=3b-a 3)Найдите модуль вектора е. 4)Найдите длину вектора n .
• 1) Запишите векторы а и b, заданные координатами точек начала А(3;-1;5) и конца В(7;4;-2), и С (0; -1; 5) и D(8; -2; 1)соответственно.
• 2)Найдите координаты векторов е и n, если е=-2a+b, n=3b-a
• 3)Найдите модуль вектора е.
• 4)Найдите длину вектора n .