Муниципальное образовательное учреждение
«Гимназия общественно-гуманитарного профиля города Тореза»
Интегрированный урок по теме
«Эта многоликая парабола»
(Квадратичная функция, ее график и свойства, 9 класс)
Интегрированный урок по математике, предмета информатика и ИКТ
Авторы:
Любимченко Ольга Викторовна
учитель математики,
Маруда Юлия Викторовна
учитель предмета информатики и ИКТ
Цели урока:
деятельностная– научить детей структуризации полученных знаний по теме «Квадратичная функция и её график», используя возможности ИКТ технологий и использовать эти знания для решения задач, входящих в раздел «Алгебра » ГИА; развивать умения перехода от частного к общему и наоборот; учить находить выход из проблемной ситуации;
содержательная – научить обобщению, видению нового знания в структуре общего курса, его связь с уже приобретенным опытом и его значение для последующего обучения; показать практическую значимость знаний учащихся, потребность связи математики с информатикой, донести знания до учащихся как можно интереснее, доступнее; развивать самостоятельность в мышлении и в учебной деятельности, формировать познавательный интерес.
Решаемые задачи:
образовательная: систематизация знаний учащихся по теме «Квадратичная функция»; формирование навыков и умений построения графиков квадратичной функции через табличный процессор MS Excel.
развивающая: развивать образное и логическое мышления учащихся; формирование математического языка; прививать интерес к математике и информатике; создать условия для формирования интереса к умению анализировать, расширению кругозора из разных предметных областей, умения анализировать и обобщать.
воспитательная: продемонстрировать возможности применения компьютеров, в частности табличного процессора MS Excel, для решения задач; воспитывать умения самостоятельно мыслить, ответственность за выполняемую работу, аккуратность при выполнении работы;
Формируемые УУД:
предметные: повторение теоретического материала по данной теме; формирование знаний и умений по изучаемому материалу, закрепление навыков построения квадратичной функции;
личностные: формирование навыков самоанализа, самоконтроля и самооценки, устойчивой мотивации к обучению;
регулятивные: определение цели учебной деятельности, осуществление поиска средств её достижения, выявление отклонений от эталона в своей работе, понимание причины ошибок;
познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме;
коммуникативные: регулирование собственной деятельности посредством речевых действий, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка.
Тип урока: Урок общеметодологической направленности (систематизации знаний).
Ожидаемый результат: в ходе урока происходит обобщение и систематизация знаний учащихся по данной теме, что создаёт более целостную картину изученного, формирует умение в многообразии заданий находить рациональный, обоснованный способ решения.
Принципы обучения:
- научности;
- системности и последовательности;
- наглядности.
Методы и приемы обучения: проблемный, фронтальный, словесно-наглядный, рефлексия.
Формы работы: индивидуальная, групповая.
Техническое обеспечение урока: компьютер, проектор, мультимедийная презентация.
Продолжительность урока: 45 минут.
Ход урока
I. Этап мотивации к учебной деятельности.
Эпиграф к уроку:
«Никто не обнимет необъятного»
Козьма Прутков
Просмотр видеоролика «Гимн параболе!»
Сколько бы мы не познавали, сколько бы мы не изучали окружающий нас мир, всегда останется что-то неизвестным, что-то неизведанным. Эпиграф к нашему сегодняшнему уроку поощряет нас не останавливаться на достигнутом, а двигаться дальше, расширяя горизонты своих знаний.
Начерченный график – это краткое и наглядное описание какого-либо процесса, или цепочки событий, или ряда наблюдений. Недаром считают, что график – это «говорящая линия», которая может много рассказать.
Умение строить графики функций не является самоцелью. Часто построение графиков связано с исследованием поведения функции. Сегодня мы займемся исследованием квадратичной функции.
Тема нашего урока «Эта многоликая парабола» (Квадратичная функция, ее график и свойства)
II. Этап постановки целей урока.
Цели урока учащиеся ставят самостоятельно.
III. Этап актуализация знаний учащихся.
Мы изучили тему «Квадратичная функция», научились строить график квадратичной функции, находить ось симметрии параболы, координаты вершины параболы, сдвиг графика вдоль ось абсцисс, сдвиг вдоль ось ординат. Сегодня мы в течение одного урока повторим эту тему, обобщим и систематизируем полученные знания, которые нам помогут успешного выполнения задания №7 и №17 из ГИА.
1.Фронтальная работа.
Какая функция называется квадратичной?
Из приведенных примеров укажите те функции, которые являются квадратичными.
у=5х+1; у=3х2-1; у=-2х2+х+3; у=x3+7x-1; у=-3х2+2х3.
Что является графиком квадратичной функции?
Какую информацию можно получить о графике квадратичной функции, зная коэффициенты квадратного трёхчлена. Работа с карточкой, заполнение лакун (проверка в парах).
Приложение 1
Карточка - опора.
1. Ветви параболы.
Если ветви параболы направлены вверх, то a___0.
Если ветви параболы направлены вниз, то a__0.
2. Точка пересечения параболы с осью (OY).
Если парабола пересекает ось OY выше оси абсцисс, то c___0.
Если парабола пересекает ось OY ниже оси абсцисс, то c___0.
3. Сдвиг параболы вдоль оси OX вправо m___0, влево m___0.
4. Точки пересечения с осью Ох
Две если D__0, касание при D___0, нет точек пересечения если D___0.
2. Работа в парах «Задачи-карточки».
Мы повторили необходимый теоретический материал, который поможет вам при выполнении заданий по карточкам. Если у вас возникнут затруднения, вы можете взять карточку подсказку или обратиться ко мне за помощью.
Приложение 2
Самостоятельная работа в парах
Установите соответствие между параметрами a, b, c, D и графиками квадратичных функций. Заполните таблицу
| №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 |
| а___0 | а___0 | а___0 | а___0 | а___0 | а___0 | а___0 | а___0 | а___0 |
| с___0 | с___0 | с___0 | с___0 | с___0 | с___0 | с___0 | с___0 | с___0 |
| b___0 | b___0 | b___0 | b___0 | b___0 | b___0 | b___0 | b___0 | b___0 |
| D__0 | D__0 | D__0 | D__0 | D__0 | D__0 | D__0 | D__0 | D__0 |
1) 2)
2) 3)
3)
4) 5)
5) 6)
6)
7) 8)
8)  9)
9) 
Ответы
Приложение 3
Самопроверка через интерактивную доску
| №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 |
| а0 | а0 | а0 | а0 | а0 | а | а | а | а |
| с0 | с0 | с0 | с0 | с=0 | с0 | с=0 | с0 | с0 |
| b | b0 | b0 | b=0 | b=0 | b=0 | b0 | b0 | b |
| D0 | D0 | D | D | D=0 | D0 | D0 | D0 | D0 |
3. Фронтальная работа. «Портрет параболы»
Приложение 4

Как называется график такого вида?
Как называется функция, график которой имеет такой вид.
Назовите область определения функции.
Назовите область значений функции.
Перечислите нули функции.
Назовите промежутки, в которых функция принимает положительные значения.
Назовите промежутки, в которых функция принимает отрицательные значения.
Назовите промежутки возрастания и убывания функции.
При каком значении х функция принимает наименьшее значение? Чему оно равно?
4. Построение параболы, повторение алгоритма построения.
Алгоритм построения графика функции. Работа в группах.
Приложение 5
Соотнести этап и описание. Проверка с помощью интерактивной доски.
|
| Найти координаты вершины параболы | | В таблице расположить вершину в середине таблицы и взять соседние симметричные значения х, посчитать значение функции в выбранных значениях х. Составим таблицу значений функции. |
|
| Заполнить таблицу значений функции | Название функции, что является графиком функции; направление ветвей параболы. | |
|
| Найти точки пересечения графика функции с осью ОХ | Отметить в координатной плоскости точки и соединить их плавной линией. | |
|
| Описать функцию. | А(m;n) по формулам: m = | |
|
| Построить график функции. | Решить уравнение ах2+ bх+с=0 |
5. Индивидуальная работа.
Приложение 6
Постройте график функции  . Найдите:
. Найдите:
а) область значений функции;
б) при каких значениях аргумента функция возрастает
III. Физкультурная минутка для глаз и для улучшения мозгового кровообращения.
VI. Учитель информатики.
«Компьютер – как мельница, что засыпаешь, то и получаешь. Если на входе чушь, то на выходе – чушь в квадрате».
Роберт Орбен
Сколько для построения графика квадратичной функции в ручную нужно приложить усилий: знание формул, выполнение расчётов, построение точек графика, использование линейки, карандаша, резинки.
Моя задача как учителя предмета информатики и ИКТ помочь вам на этом этапе упростить вашу работу по построению графиков функций.
Мы научимся с помощью компьютера строить диаграммы и графики очень быстро и просто в курсе 6 класса, с помощью программного обеспечения MSWord и MSEXСEL.
Сегодня с помощью MSEXСEL построим график квадратично функции.
Алгоритм построения графиков и диаграммы
Создать таблицу с числовыми данными
Выделить необходимый диапазон данных
Запустить мастер диаграмм
Выбрать тип диаграммы
Задать основные и дополнительные параметры диаграммы (выполнить шаги 1 - 4)
Форматировать и редактировать области диаграммы, если это необходимо
Приложение 7
Практическая часть
Инструктаж по технике безопасности при работе за персональным компьютером.
Задание1. Построить график функции
Y = 0,5x2 + 3х + 0,5
Диапазон изменения аргумента – [–7;1] с шагом 1
Алгоритм выполнения задания: подготовка таблицы
1. Перейдите на Лист1, переименуйте Лист1 в «Графики»:
щелкните правой клавишей мыши на ярлыке Лист1 – вызов контекстного меню;
выберите команду Переименовать.

Рис 1.
2. Подготовьте на листе «Графики» таблицу согласно рис 1. введите в ячейки В6:С6 названия столбцов заполните столбец аргументов (х) от –7 до 1 с шагом 1. Для этого воспользуйтесь любым известным вам способом автозаполнения диапазона. (Вкладка ГЛАВНОЕ- редактировать- заполнение.)
3. Заполните столбцы функций, т. е. введите в столбцы значения функций в соответствующих точках. Для этого введите самостоятельно в ячейки С7 формулу, математическая запись которых, (=0,5*В7^2+3*В7+0,5)
4. Скопируйте формулы в остальные ячейки таб. (используйте маркер заполнения).
5. Выделите диапазон данных для построения графиков С7:С15.
6. Постройте графики, используя Мастер диаграмм: тип диаграммы – точечная с гладкими кривыми.
Высокий уровень. Отредактируйте графики согласно рис. 1 и сохраните изменения в файле. Представьте результаты работы.
Цвет функции Y3(x) сделать желтым. Задать название графика – «Графики функций».
Здание 2. Рассмотрим одно из заданий ГИА по математике.
Постройте график функции  . Пользуясь графиком, найдите:
. Пользуясь графиком, найдите:
а) промежуток убывания функции;
б) при каких значениях х функция принимает отрицательные значения.
VI. Этап рефлексии
В заключении я хочу рассказать вам такую притчу:
«Шёл мудрец, а навстречу ему три человека, которые везли под горючим солнцем тележки с камнями для строительства. Мудрец остановился и задал вопрос каждому. У первого спросил: ʺА что ты делал целый день? ʺ И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: ʺА что ты делал целый день?ʺ, и тот ответил: ʺА я добросовестно выполнял свою работуʺ. А третий улыбнулся, его лицо засветилось радостью и удовольствием: ʺА я принимал участие в строительстве храма!ʺ
- Ребята! Давайте мы попробуем с вами оценить каждый свою работу на уроке. Выберите картинку соответствующую вашей работе не уроке.
- Кто работал как первый человек?

- Кто работал добросовестно?

- Кто принимал участие в строительстве храма знаний?

VII. Домашнее задание
Построить и исследовать графики квадратичной функции с помощью алгоритмов по предметам математики и информатики.
Постройте график функции
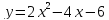 . Найдите:
. Найдите:
а) область значений функции;
б) при каких значениях аргумента функция убывает.
Постройте график функции
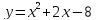 . Пользуясь графиком, найдите:
. Пользуясь графиком, найдите:
а) промежуток убывания функции;
б) при каких значениях х функция принимает положительные значения.
Постройте график функции
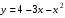 . Найдите:
. Найдите:
а) при каких значениях аргумента значения функции положительные;
б) при каких значениях аргумента функция убывает.
Постройте график функции
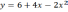
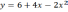 . Найдите:
. Найдите:
а) область значений функции;
б) при каких значениях аргумента функция убывает.
Постройте график функции
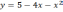
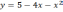 . Пользуясь графиком, найдите:
. Пользуясь графиком, найдите:
а) область значений функции;
б) промежуток убывания функции.


 1469
1469 82
82 и n = у(m). Прямая x=m является осью симметрии параболы.
и n = у(m). Прямая x=m является осью симметрии параболы.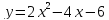 . Найдите:
. Найдите: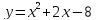 . Пользуясь графиком, найдите:
. Пользуясь графиком, найдите: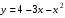 . Найдите:
. Найдите: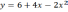
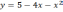
 Интегрированный урок по теме «Эта многоликая парабола» (Квадратичная функция, ее график и свойства, 9 класс) Интегрированный урок по математике, предмета информатика и ИКТ
Интегрированный урок по теме «Эта многоликая парабола» (Квадратичная функция, ее график и свойства, 9 класс) Интегрированный урок по математике, предмета информатика и ИКТ 